logo

Okrąg wpisany w trójkąt

Definicja 1

Okrąg wpisany w trójkąt to okrąg, który jest styczny do wszystkich boków trójkąta (środek okręgu jest równo oddalony od boków trójkąta).

Uwaga 1

Zamiast mówić że okrąg został wpisany w trójkąt, możemy powiedzieć, że trójkąt został opisany na okręgu.

Twierdzenie 1

Dwusieczne kątów wewnętrznych w trójkącie przecinają się w jednym punkcie będącym środkiem okręgu wpisanego w ten trójkąt.

Dodatkowo, długość promienia okręgu wpisanego w trójkąt jest równa odległości środka okręgu od dowolnego boku tego trójkąta.

Twierdzenie 2

Długość rr promienia okręgu wpisanego w trójkąt o bokach długości a,b,ca,b,c dany jest wzorem:

r=(p−a)(p−b)(p−c)p\begin{aligned} \displaystyle r&=\sqrt{\frac{(p-a)(p-b)(p-c)}{p}}\\ \end{aligned}
(0)

lub

r=2Pa+b+c,r= \frac{2P}{a+b+c} ,
(0)

lub

r=Ppr= \frac{P}{p}
(0)

gdzie PP to pole trójkąta, a pp to połowa obwodu tego trójkąta:

p=a+b+c2p=\frac{a+b+c}{2}
(0)

Twierdzenie 3

Pole trójkąta o obwodzie a+b+ca+b+c opisanego na okręgu o promieniu długości rr wynosi:

P=a+b+c2⋅rP=\frac{a+b+c}{2}\cdot r
(0)

Twierdzenie 4

Środek okręgu wpisanego w trójkąt równoramienny leży na wysokości poprowadzonej na podstawę.

Twierdzenie 5

Środkiem okręgu wpisanego w trójkąt równoboczny jest punkt przecięcia się jego wysokości, a promień tego okręgu jest równy jednej trzeciej wysokości trójkąta:

r=13h=a36r= \frac{1}{3}h= \frac{a\sqrt{3}}{6}
(0)
Twierdzenie 6

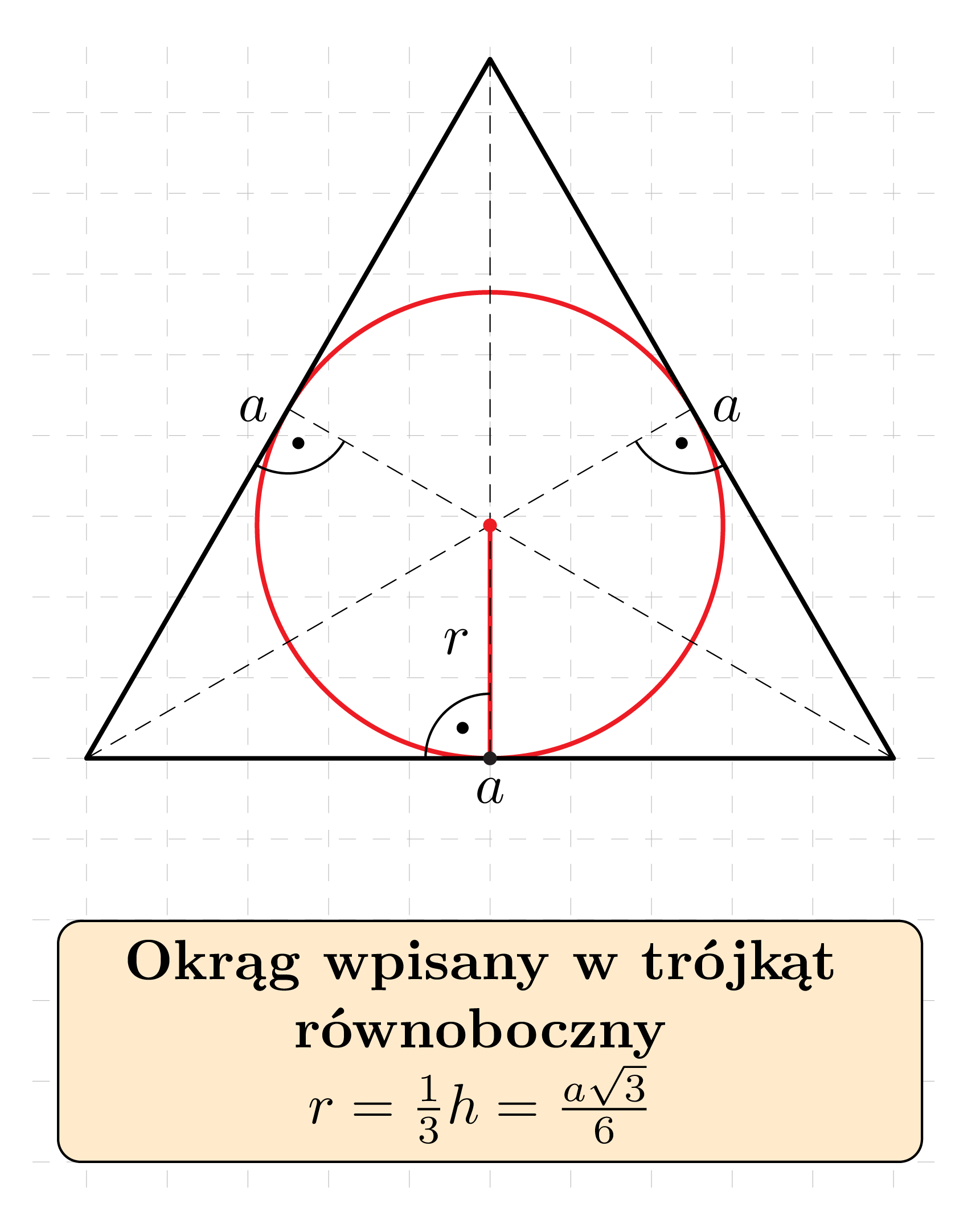
Długość rr promienia okręgu wpisanego w trójkąt prostokątny o przyprostokątnych długości aa i bb oraz przyprostokątnej długości cc dany jest wzorem:

r=a+b−c2r=\frac{a+b-c}{2}
(0)