Odcinkiem o końcach w punktach A=\left(x_A,y_A\right) i B=\left(x_B,y_B\right) nazywamy zbiór wszystkich punktów P=\left(x,y\right), które leżą między punktami A i B, czyli:
Znając współrzędne punktów A i B możemy obliczyć odległość między nimi lub inaczej, długość odcinka AB. Wzór na długość odcinka wynika z Twierdzenia Pitagorasa.
Odległość między punktami A=(x_A,y_A) i B=(x_B, y_B) (tj. długość odcinka AB) w układzie współrzędnych wyraża się wzorem:
W szczególności:
jeżeli y_A=y_B (odcinek AB jest równoległy do osi OX), to
|AB|=|x_B-x_A|jeżeli x_A=x_B (odcinek AB jest równoległy do osi OY), to
|AB|=|y_B-y_A|

Odległość między prostymi k i l danych równaniami:
gdzie A^2+B^2\neq 0 wyraża się wzorem:
Środkiem odcinka AB o współrzędnych A=(x_A,y_A) i B=(x_B, y_B) jest punkt:

Odległość punktu P=(x_0,y_0) od prostej k danej równaniem ogólnym:
wyraża się wzorem:

Współrzędne środka ciężkości S trójkąta ABC o współrzędnych A=\left(x_A,y_A\right), B=(x_B,y_B) i C=(x_C,y_C) wyrażają się wzorem:
Równanie postaci:
nazywamy równaniem kierunkowym prostej, gdzie a to współczynnik kierunkowy, a b - wyraz wolny.
Kątem nachylenia prostej do osi OX nazywamy kąt którego wierzchołkiem jest punkt przecięcia się tej prostej z osią OX, a ramionami część prostej znajdująca się nad osia OX oraz półprosta zawierająca się w osi OX.

Prosta y=ax+b jest nachylona do osi OX pod kątem \alpha\in[0^\circ ,180^\circ )\setminus\{90^\circ \}, takim że \tg\alpha=a.

Równanie kierunkowe prostej o danym współczynniku kierunkowym 𝑎, która przechodzi przez punkt P=\left(x_0,y_0\right) to:
Kąt nachylenia prostej w postaci ogólnej y=ax+b do osi OX jest:
ostry, jeśli a>0,
zerowy (prosta jest równoległa do osi OX), jeśli a =0,
rozwarty, jeśli a<0.
.png)
Kąt ostry \alpha utworzony przez dwie nieprostopadłe proste o równaniach
spełnia równanie:
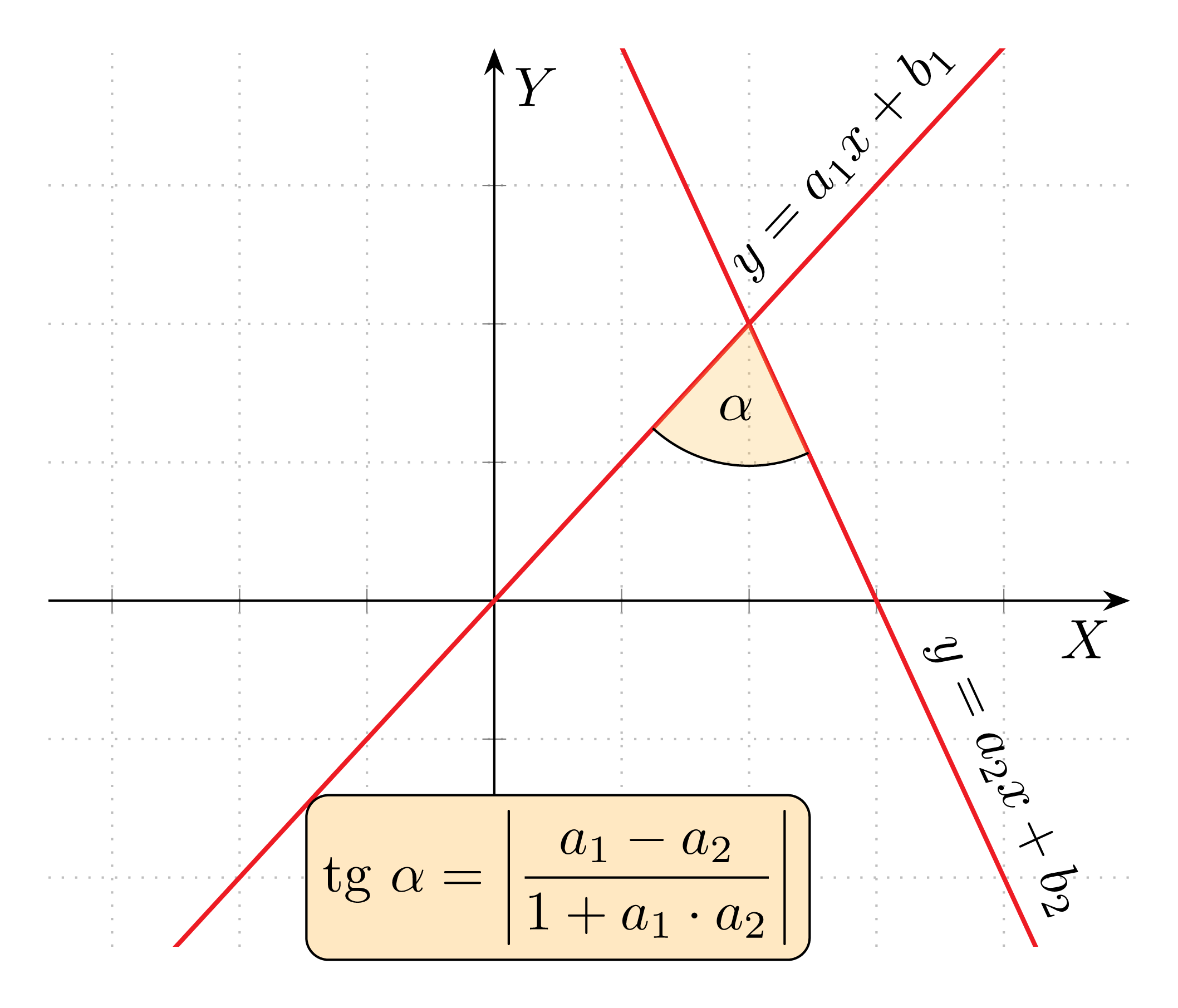
Wiemy już, że współczynnik kierunkowy prostej zależy od kąta nachylenia tej prostej do osi OX:
Żeby dwie proste były równoległe, nie mogą się przecinać, czyli ich kąt nachylenia do osi OX musi być taki sam, a tym samym współczynniki kierunkowe muszą być równe:
Dwie proste o równaniach y=a_1x+b_1 oraz y=a_2x+b_2, gdzie a_1\neq0 i a_2\neq0 są równoległe wtedy i tylko wtedy, gdy a_1=a_2.

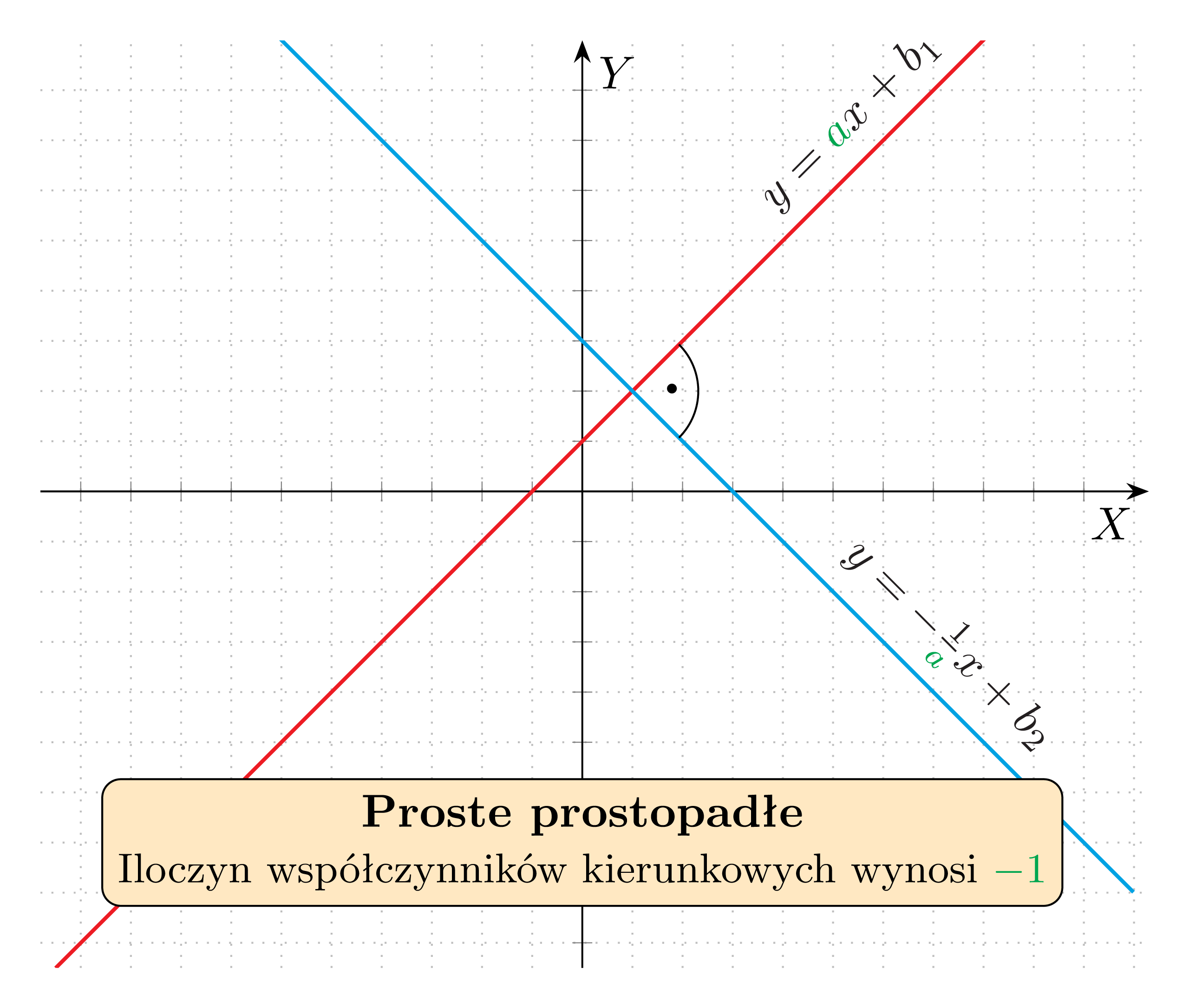
Niech dane będą dwie proste prostopadłe:

Mamy:
Zatem
Dwie proste o równaniach y=a_1x+b_1 oraz y=a_2x+b_2 są prostopadłe wtedy i tylko wtedy, gdy a_1\cdot a_2=-1.
Równanie prostej przechodzącej przez punkty o współrzędnych (x_A,y_A) oraz (x_B,y_B) gdzie x_A\neq x_B, dane jest wzorem:
lub
lub:
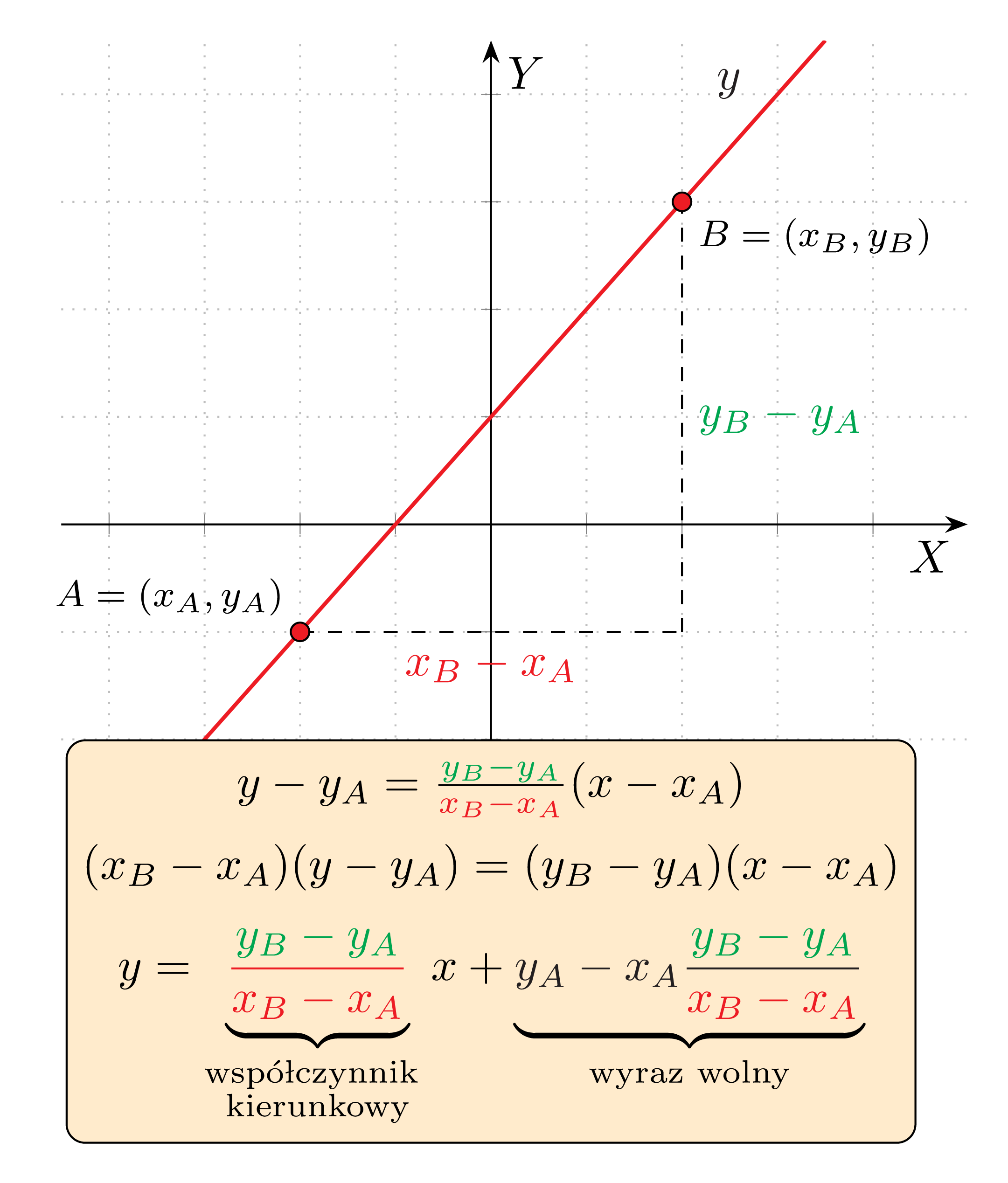
Jeśli powyższy wzór wydaje Ci się skomplikowany to nie bój się - w praktyce najczęściej wyznaczamy równanie prostej przechodzącej przed dwa punkty wprost z definicji prostej, podstawiając kolejno dwa podane punkty i otrzymując układ równań.
Warto jednak zapamiętać wzór
i w razie potrzeby przekształcać go w celu wyznaczenia równania prostej.
Równanie postaci
gdzie A^2+B^2\neq0 nazywamy równaniem ogólnym prostej.
Dwie proste o równaniach ogólnych A_1x+B_1+C_1=0 oraz A_2x+B_2+C_2=0 gdzie A_1^2+B_1^2\neq0 i A_2^2+B_2^2\neq0 są prostopadłe wtedy i tylko wtedy, gdy A_1A_2+ B_1B_2=0.

Dwie proste o równaniach ogólnych A_1x+B_1+C_1=0 oraz A_2x+B_2+C_2=0 gdzie A_1^2+B_1^2\neq0 i A_2^2+B_2^2\neq0 są równoległe wtedy i tylko wtedy, gdy A_1B_2+ A_2B_1=0.


