Liczba a\in\mathbb{Z} jest podzielna przez liczbę b\in\mathbb{Z-\{0}\} gdy dzieli się przez nią bez reszty, tj. jeśli istnieje taka liczba c\in\mathbb{Z}, że
Liczbę b nazywamy dzielnikiem liczby a i symbolicznie zapisujemy b|a co czytamy “b jest dzielnikiem a”, “liczba b dzieli liczbę a” lub “liczba a jest podzielne przez b”. Mówimy też, że a jest wielokrotnością liczby b.
Dodatkowo, wyrażenie a\nmid b czytamy “liczba a nie dzieli liczby b” lub “liczba b nie jest podzielna przez a”.
dzielniki liczby 12 to 1,2,3,4,6,12.
dzielniki liczby 15 to 1,3,5,15.
dzielniki liczby 23 to 1 i 23.
Aby sprawdzić czy dana liczba jest dzielnikiem innej liczby, możemy wykonać dzielenie i sprawdzić czy reszta jest równa 0. Alternatywnie, w niektórych przypadkach możemy skorzystać z tzw. cech podzielności liczb które pozwalają nam odpowiedzieć na to pytanie bez konieczności wykonania dzielenia na całej liczbie. Cechy te ułatwiają znalezienie dzielników, zwłaszcza dużych liczb.
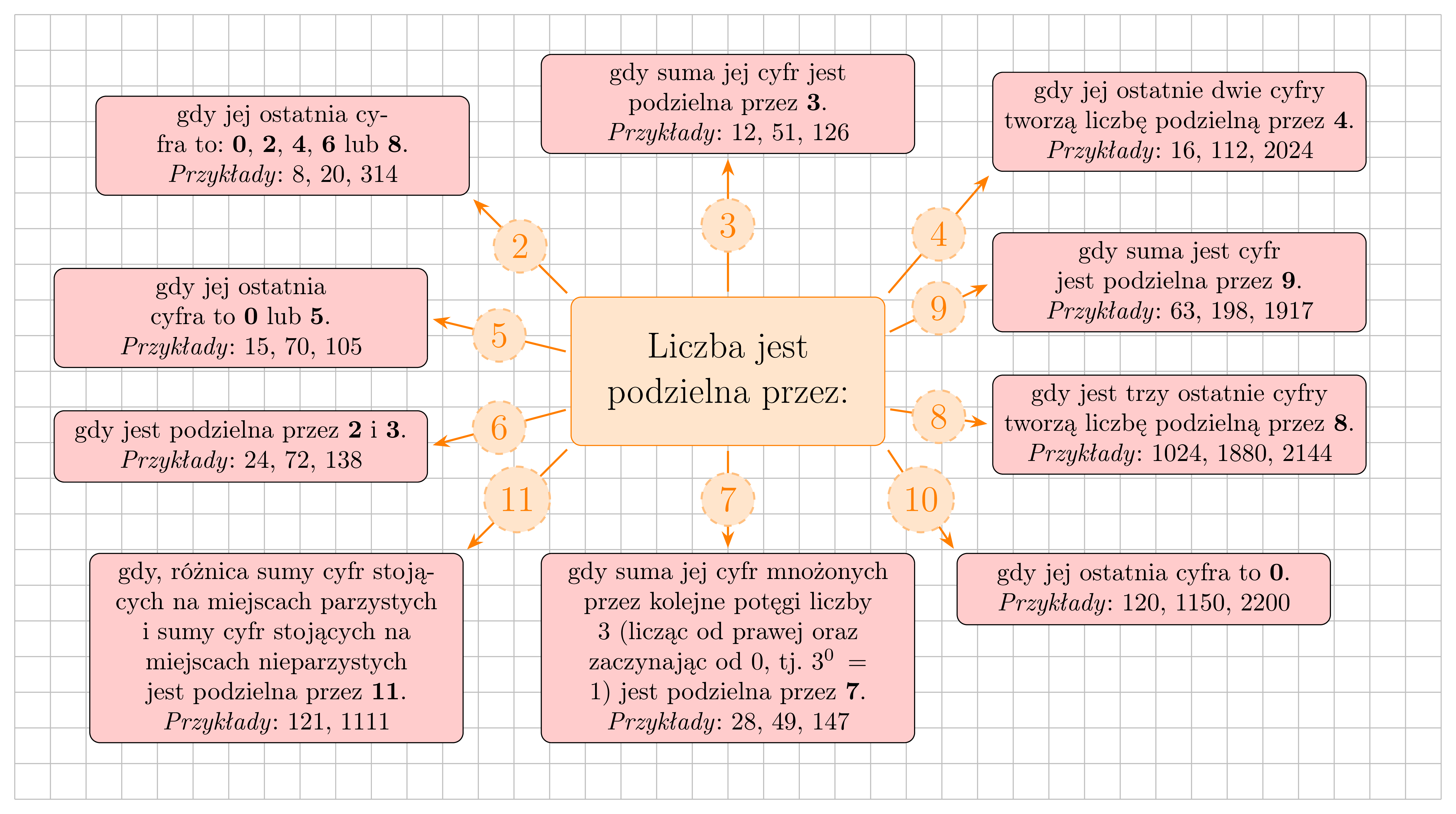
Dla liczb od 2 do 11 obowiązują następujące reguły podzielności:
Liczba | Reguła |
2 | Ostatnia cyfra to 0, 2, 4, 6, 8 |
3 | Suma cyfr jest podzielna przez 3 |
4 | Dwie ostatnie cyfry tworzą liczbę podzielną przez 4 |
5 | Ostatnia cyfra to 0 lub 5 |
6 | Jest podzielna zarówno przez 2 oraz 3 |
7 | Suma cyfr mnożonych przez kolejne potęgi liczby 3 (licząc od prawej oraz zaczynając od potęgi 0, tj. 3^0=1) jest podzielna przez 7. Dodatkowo (dla dużych liczb): różnica między liczbą składającą się z trzech ostatnich cyfr liczby, a liczbą wyrażoną pozostałymi cyframi tej liczby (lub odwrotnie) dzieli się przez 7 |
8 | Trzy ostatnie cyfry tworzą liczbę podzielną przez 8 |
9 | Suma cyfr jest podzielna przez 9 |
10 | Ostatnia cyfra to 0 |
11 | Różnica sumy cyfr stojących na miejscach parzystych i sumy cyfr stojących na miejscach nieparzystych jest podzielna przez 11. |
Ogólnie, liczba jest podzielna przez 10^n itd. gdy jej ostatnie n cyfr to zera.
Niektóre z cech podzielności można łatwo dostrzec wypisując kolejne wielokrotności liczby przez która chcemy dzielić:
2: 2,4,6,8,10,12,14,16,18,20,\ldots - ostatnia cyfra to 0,2,4,6 lub 8
5,10,15,20,25,30,\ldots - ostatnia cyfra to 0 lub 5
10,20,30,40,50,\ldots - ostatnia cyfra to 0
W większości przypadków dostrzeżenie zależności nie jest takie proste:
3,6,9,12,15,18,21,24,27,30,\ldots - zauważmy, że suma cyfr każdej z liczb jest liczbą podzielną przez 3: 3,6,9,3,6,9,3,6,9,3.
9,18,27,36,45,54,63,72,81,90,99 - suma cyfr jest podzielna przez 9.
4,8,12,16,\ldots,96,100,104,108,\ldots,992,996,1000 - liczba utworzona z dwóch ostatnich cyfr jest podzielne przez 4.
Zobaczmy jak zastosować cechy podzielności liczb na poniższych przykładach:
Liczba \textcolor{green}{1}\textcolor{orange}{2}\textcolor{brown}{6} dzieli się przez 3 ponieważ \textcolor{green}{1}+\textcolor{orange}{2}+\textcolor{brown}{6}=9 oraz 3|9.
Liczba 1\color{orange}{12} dzieli się przez 4, ponieważ 4|12.
Liczba 10\textcolor{orange}{5} dzieli się przez 5, jej ostatnia cyfra to 5.
Liczba \textcolor{green}{1}\textcolor{orange}{3}\textcolor{brown}{8} dzieli się przez 6 ponieważ dzieli się przez 2 oraz dzieli się przez 3 (\textcolor{green}{1}+\textcolor{orange}{3}+\textcolor{brown}{8}=12 oraz 3|12).
Liczba \textcolor{green}{1}\textcolor{orange}{4}\textcolor{brown}{7} dzieli się przez 7 ponieważ:
7\cdot3^0+4\cdot3^1+1\cdot 3^2=28\land 7|28(0)Liczba 2\textcolor{orange}{144} dzieli się przez 8 ponieważ 8|144.
Liczba \textcolor{green}{1}\textcolor{orange}{9}\textcolor{brown}{1}\textcolor{teal}{7} jest podzielna przez 9 ponieważ
\textcolor{green}{1}+\textcolor{orange}{9}+\textcolor{brown}{1}+\textcolor{teal}{7}=18 \land 9|18(0)Liczba 220\color{orange}0 jest podzielna przez 10, ponieważ jej ostatnia cyfra to 0.
Liczba \color{green}6\color{orange}1\color{brown}6 jest podzielna przez 11, ponieważ
\textcolor{orange}1-(\textcolor{green}{6}+\textcolor{brown}{6})=-11\land 11|(-11)(0)
Podzielność liczby n przez liczbę m zapisujemy symbolicznie m|n.
Alternatywnie, możemy również skorzystać z zapisu
dla pewnego k\in\mathbb{Z}. Jeśli n nie jest ustalone i chcemy symbolicznie zapisać zbiór wszystkich liczb podzielnych przez m\in\mathbb{Z}, możemy to zrobić następująco:
W szczególności \mathbb{Z_2} oznacza zbiór liczb całkowitych podzielnych przez 2 (zbiór liczb parzystych), a \mathbb{Z_5} zbiór liczb całkowitych podzielnych przez 5.
Aby symbolicznie zapisać zbiór wszystkich liczb całkowitych które przy dzieleniu przez m\in\mathbb{Z} zwracają resztę r\in\mathbb{N} możemy skorzystać z zapisu:
W szczególności \mathbb{Z_{2,1}} oznacza zbiór liczb całkowitych które przy dzieleniu przez dwa zwracają resztę 1 (zbiór liczb nieparzystych).
Ile razy więcej, ile razy mniej
Z pojęciem mnożenia i dzielenia wiąże się naturalne pytanie na które możemy odpowiedzieć wykorzystując właśnie te dwie operacje matematyczne:
“Ile razy dana liczba jest mniejsza/większa od innej liczby?”
Liczba 10 jest dwa razy większa od liczby 5, ponieważ 5 \cdot 2=10.
Liczba 16 jest 3 razy mniejsza od liczby 48, ponieważ 48:3=16.
4 razy więcej niż 3 to 12, ponieważ 3 \cdot 4=12.
5 razy mniej niż 30 to 6 ponieważ 30:5=6.
Zauważ, że zamiast mówić że liczba 20 jest 4 razy większa od liczby 5, możemy równoważnie powiedzieć, że liczba 5 jest o 4 razy mniejsza od liczby 20.
Dodatkowo, w praktyce często zamiast mówić że coś jest dwa (trzy) razy większe/mniejsze, mówimy że coś jest dwukrotnie (trzykrotnie) większe/mniejsze - analogicznie dla większych liczb (czterokrotnie, pięciokrotnie, dziesięciokrotnie, …).