Doświadczenie losowe

Doświadczeniem losowym nazywamy zdarzenie lub proces, który można przeprowadzić w określonych warunkach, a jego wynik jest nieprzewidywalny, ale należy do pewnego zbioru wszystkich możliwych wyników zwanego przestrzenią zdarzeń elementarnych i oznaczanego symbolem $\Omega=\left\{\omega_1,\omega_2,\ldots\right\}$\Omega=\left\{\omega_1,\omega_2,\ldots\right\}. Pojedynczy wynik doświadczenia losowego nazywamy zdarzeniem elementarnym i oznaczamy $\omega$\omega.

Zdarzeniem losowym nazywamy dowolny podzbiór przestrzeni zdarzeń elementarnych $\Omega=\left\{\omega_1,\omega_2,\ldots,\omega_n\right\}$\Omega=\left\{\omega_1,\omega_2,\ldots,\omega_n\right\}. Zdarzenia losowe oznaczamy wielkimi literami $A,B,C,\ldots$A,B,C,\ldots. Zbiór $\Omega$\Omega nazywamy zdarzeniem pewnym, zbiór pusty $\emptyset$\emptyset nazywamy zdarzeniem niemożliwym, natomiast każdy element zdarzenia losowego nazywamy wynikiem (zdarzeniem elementarnym) sprzyjającym zdarzeniu $A$A.

Przykłady: $A=\left\{\omega_1,\omega_3\right\}$A=\left\{\omega_1,\omega_3\right\}, $B=\emptyset$B=\emptyset, $C=\Omega$C=\Omega, $D=\left\{w_2\right\}$D=\left\{w_2\right\}.

Doświadczeniem losowym jest np. rzut kostką, przestrzenią zdarzeń elementarnych jest zbiór $\left\{1,2,3,4,5,6\right\}$\left\{1,2,3,4,5,6\right\}. Zdarzeniem losowym jest np. zdarzenie polegające na wyrzuceniu parzystej liczby oczek: $\left\{2,4,6\right\}$\left\{2,4,6\right\}. Zdarzeniami elementarnymi sprzyjającymi takiego zdarzeniu losowego są: $2,4,6$2,4,6.

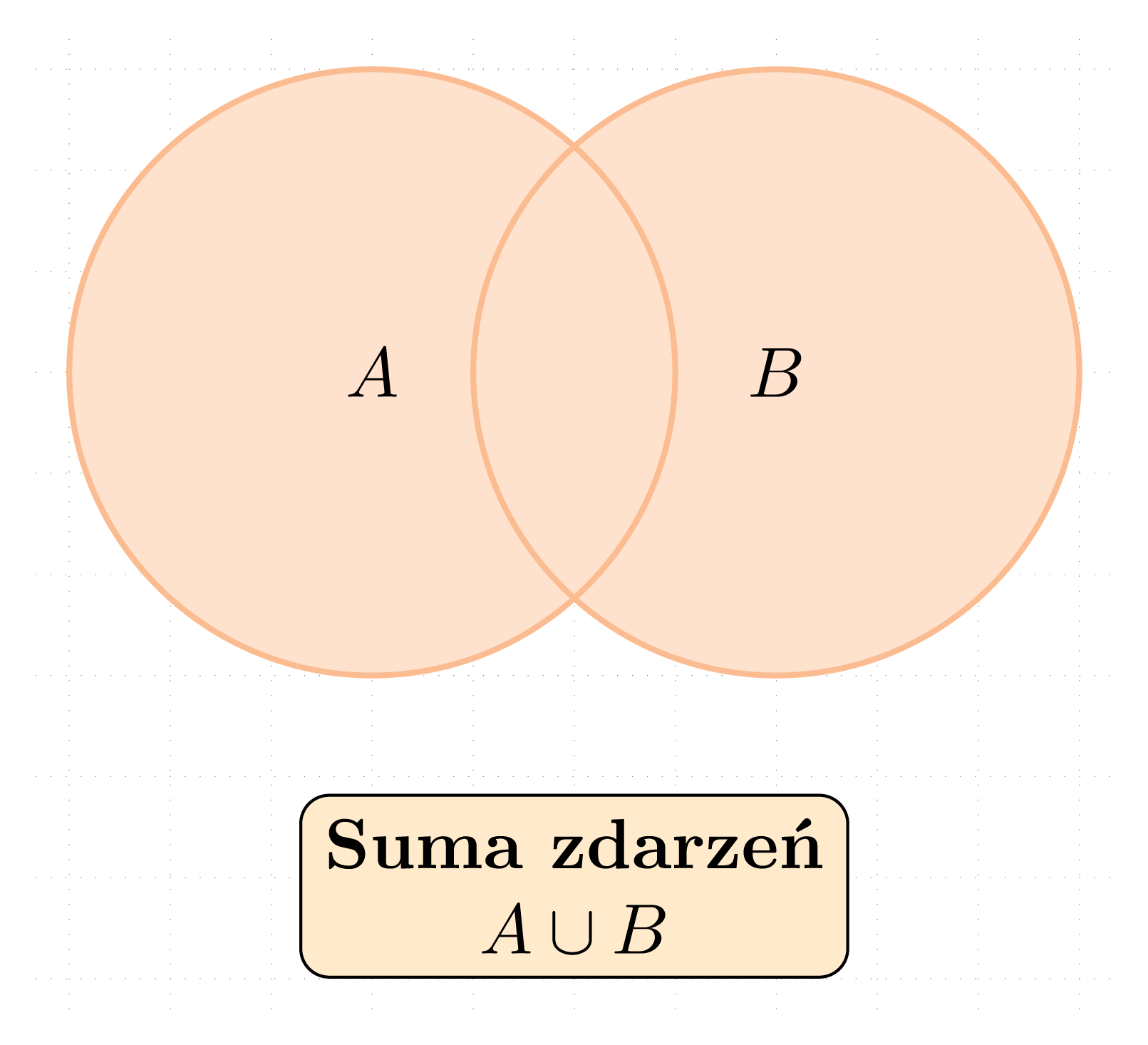
Sumą zdarzeń $A$A i $B$B, $A,B\subset\Omega$A,B\subset\Omega nazywamy zdarzenie $A\cup B$A\cup B będące zbiorem zdarzeń elementarnych przestrzeni $\Omega$\Omega, które sprzyjają przynajmniej jednemu ze zdarzeń $A$A i $B$B.

Różnicą zdarzeń $A$A i $B$B, $A,B\subset\Omega$A,B\subset\Omega nazywamy zdarzenie $A\backslash B$A\backslash B będące zbiorem zdarzeń elementarnych przestrzeni $\Omega$\Omega, które sprzyjają zdarzeniu $A$A, ale nie sprzyjają zdarzeniu $B$B.

Iloczynem zdarzeń $A$A i $B$B, $A,B\subset\Omega$A,B\subset\Omega nazywamy zdarzenie $A\cap B$A\cap B będące zbiorem zdarzeń elementarnych przestrzeni $\Omega$\Omega, które sprzyjają zarówno zdarzeniu $A$A jak i $B$B.

Mówimy, że zdarzenia $A$A i $B$B są rozłączne lub wykluczają się (nie mogą zajść jednocześnie), jeżeli $A\cap B=\emptyset$A\cap B=\emptyset.

ówimy że zdarzenia $A$A i $B$B są identyczne, jeżeli $A=B$A=B.

Zdarzeniem przeciwnym do zdarzenia $A$A nazywamy zdarzenie $A'=\Omega\backslash A$A'=\Omega\backslash A.

Mówimy, że zdarzenie $A$A zawiera się w zdarzeniu $B$B (lub pociąga za sobą zdarzenie $B$B) $A\subset B$A\subset B, jeżeli wszystkie elementy zdarzenia $A$A należą do zdarzenia $B$B.