Działania na zbiorach

Diagram Venna to graficzny sposób przedstawienia zależności między zbiorami, zazwyczaj przyjmujących postać figur geometrycznych na płaszczyźnie. Zbiory reprezentowane są na ogół przez elipsy, umieszczone wewnątrz prostokąta oznaczającego całą przestrzeń. Aby ułatwić rozpoznanie relacji między zbiorami, takich jak inkluzja, suma czy iloczyn, figury te są wyróżniane różnymi teksturami i kolorami.

Sumą zbiorów $A$A i $B$B nazywamy zbiór elementów, które należą do co najmniej jednego z tych zbiorów. Sumę zbiorów $A$A i $B$B oznaczamy $A\cup B$A\cup B.

Wyrażenie $x\in A\cup B$x\in A\cup B czytamy: “element $x$x należy do zbioru $A$A lub do zbioru $B$B.”

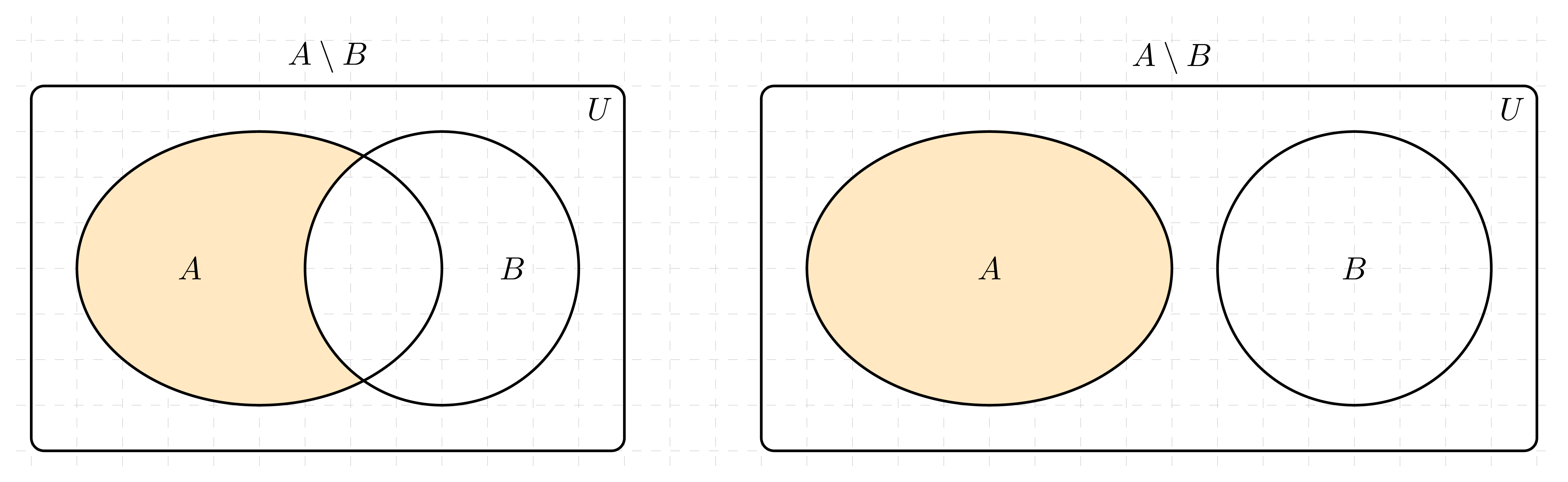
Różnicą zbiorów $A$A i $B$B nazywamy zbiór elementów, które należą do zbioru $A$A i nie należą do zbioru $B$B. Różnicę zbiorów $A$A i $B$B oznaczamy $A\backslash B$A\backslash B lub $A-B$A-B.

Iloczynem (częścią wspólną) zbiorów $A$A i $B$B nazywamy zbiór elementów, które należą jednocześnie do obu tych zbiorów. Iloczyn zbiorów $A$A i $B$B oznaczamy $A\cap B$A\cap B.

Mówimy, że zbiory $A$A i $B$B są rozłączne, gdy nie mają części wspólnej, czyli $A\cap B=\emptyset$A\cap B=\emptyset.

Niech $A$A i $B$B będą zbiorami. Wówczas

Innymi słowy:

• Dopełnienie części wspólnej zbiorów $A$A i $B$B jest sumą dopełnień tych zbiorów.

• Dopełnienie sumy zbiorów $A$A i $B$B jest częścią wspólną dopełnień tych zbiorów.

Własności te nazywamy odpowiednio I oraz II prawem De Morgana.

Dopełnieniem zbioru $A$A do przestrzeni $U$U nazywamy zbiór elementów przestrzeni $U$U, które nie należą do zbioru $A$A, tj. różnicę zbiorów $U$U i $A$A. Dopełnienie zbioru oznaczamy symbolem $A'$A'.

Iloczynem kartezjańskim zbiorów $A$A i $B$B nazywamy zbiór wszystkich par $(a,b)$(a,b) takich, że $a\in A$a\in A oraz $b\in B$b\in B. Zbiór ten oznaczamy $A\times B$A\times B.

Iloczyn kartezjański zbiorów liczb całkowitych $\mathbb{Z}\times\mathbb{Z}$\mathbb{Z}\times\mathbb{Z} nazywamy zbiorem kratowym.

Różnicą symetryczną zbiorów $A$A i $B$B nazywamy zbiór składający się z elementów należących do dokładnie jednego ze zbiorów $A$A i $B$B:

Równoważnie:

Niech $A$A i $B$B będą zbiorami. Wówczas:

• przemienność dodawania:

  $$A\cup B=B\cup A$$

  A\cup B=B\cup A(0)

• przemienność mnożenia:

  $$A\cap B=B\cap A$$

  A\cap B=B\cap A(0)

• łączność dodawania

  $$(A\cup B)\cup C = A\cup (B\cup C)$$

  (A\cup B)\cup C = A\cup (B\cup C)(0)

• łączność mnożenia:

  $$(A\cap B)\cap C=A\cap (B\cap C)$$

  (A\cap B)\cap C=A\cap (B\cap C)(0)

• rozdzielność dodawania zbiorów względem mnożenia:

  $$A\cup (B\cap C)=(A\cup B)\cap (A\cup C)$$

  A\cup (B\cap C)=(A\cup B)\cap (A\cup C)(0)

• rozdzielność mnożenia zbiorów względem dodawania:

  $$A\cap (B\cup C)=(A\cap B)\cup (A\cap C)$$

  A\cap (B\cup C)=(A\cap B)\cup (A\cap C)(0)

• odejmowanie zbiorów:

  $$A\setminus B=A\cap B'$$

  A\setminus B=A\cap B'(0)