Trygonometria to gałąź matematyki badająca relacje między długościami boków a kątami wewnętrznymi trójkątów. Jej rozwinięciem są funkcje trygonometryczne, które odgrywają istotną rolę w analizie matematycznej.
Funkcje trygonometryczne kąta ostrego \alpha — sinus, cosinus, tangens i cotangens — definiuje się na podstawie proporcji między bokami trójkąta prostokątnego.
Sinusem kąta ostrego \alpha w trójkącie prostokątnym nazywamy stosunek długości przyprostokątnej leżącej naprzeciwko kąta \alpha do długości przeciwprostokątnej:
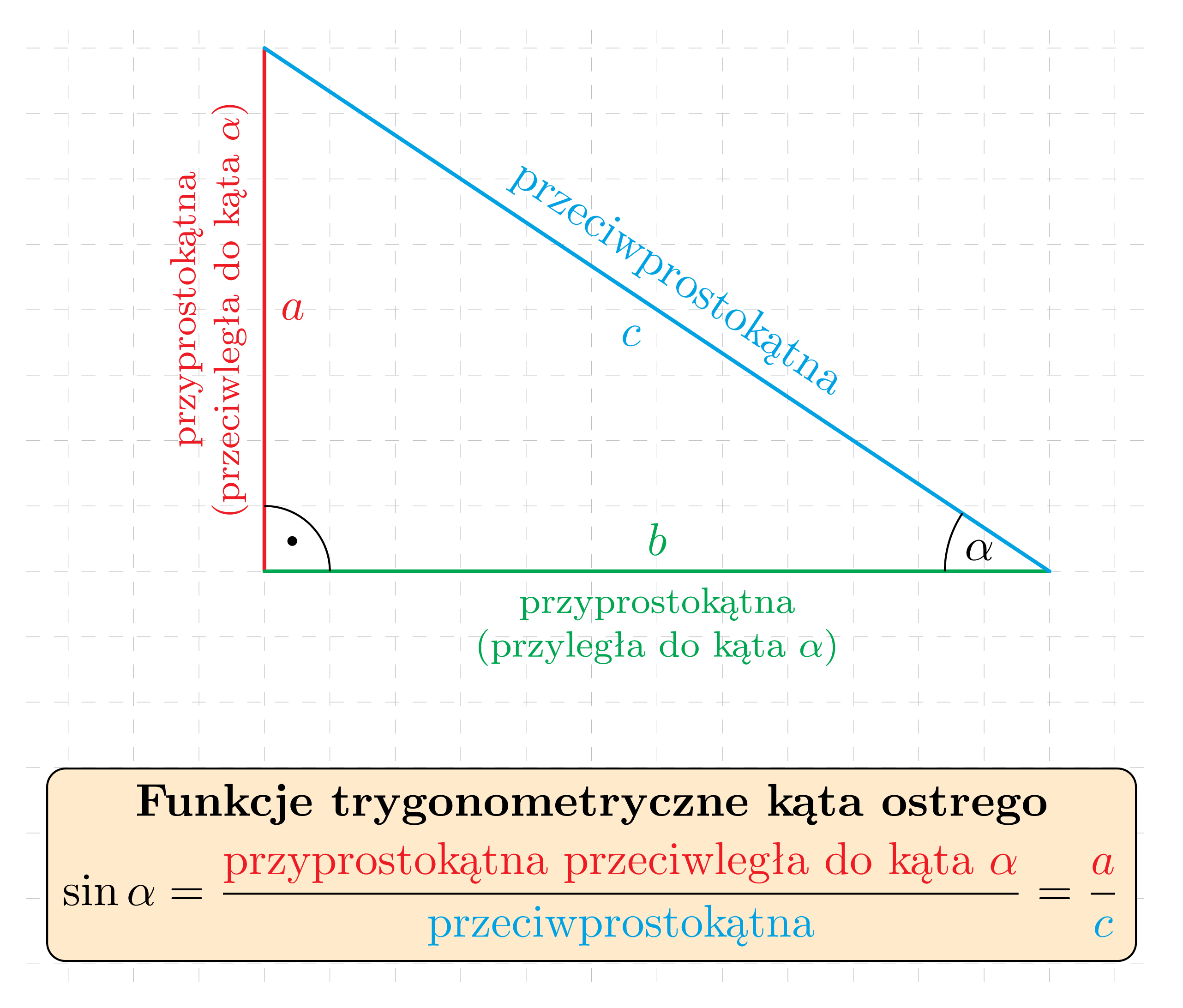
Cosinusem kąta ostrego \alpha w trójkącie prostokątnym nazywamy stosunek długości przyprostokątnej leżącej przy kącie \alpha do długości przeciwprostokątnej:
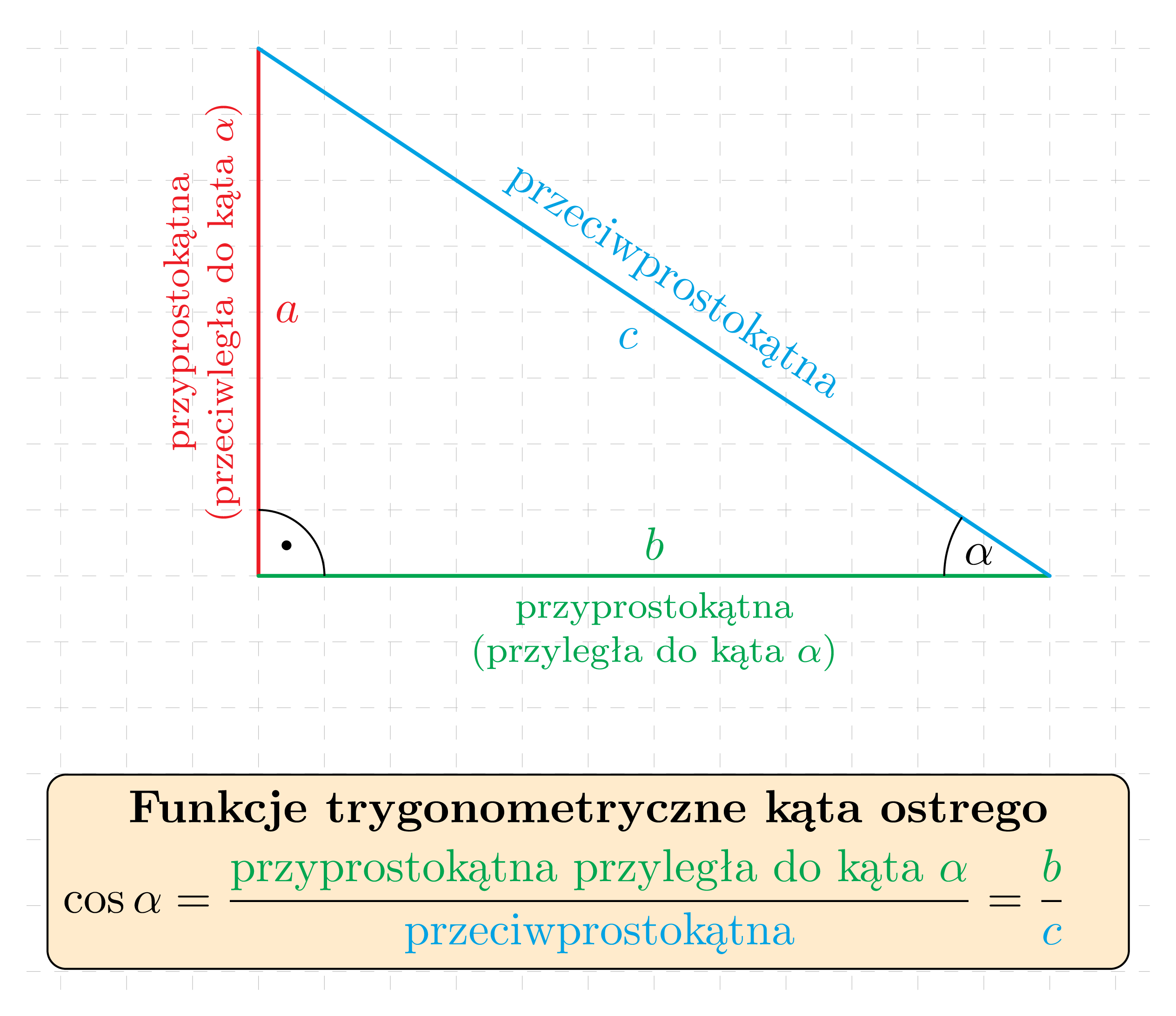
Tangensem kąta ostrego \alpha w trójkącie prostokątnym nazywamy stosunek długości przyprostokątnej leżącej naprzeciwko kąta \alpha do długości przyprostokątnej leżącej przy kącie \alpha:
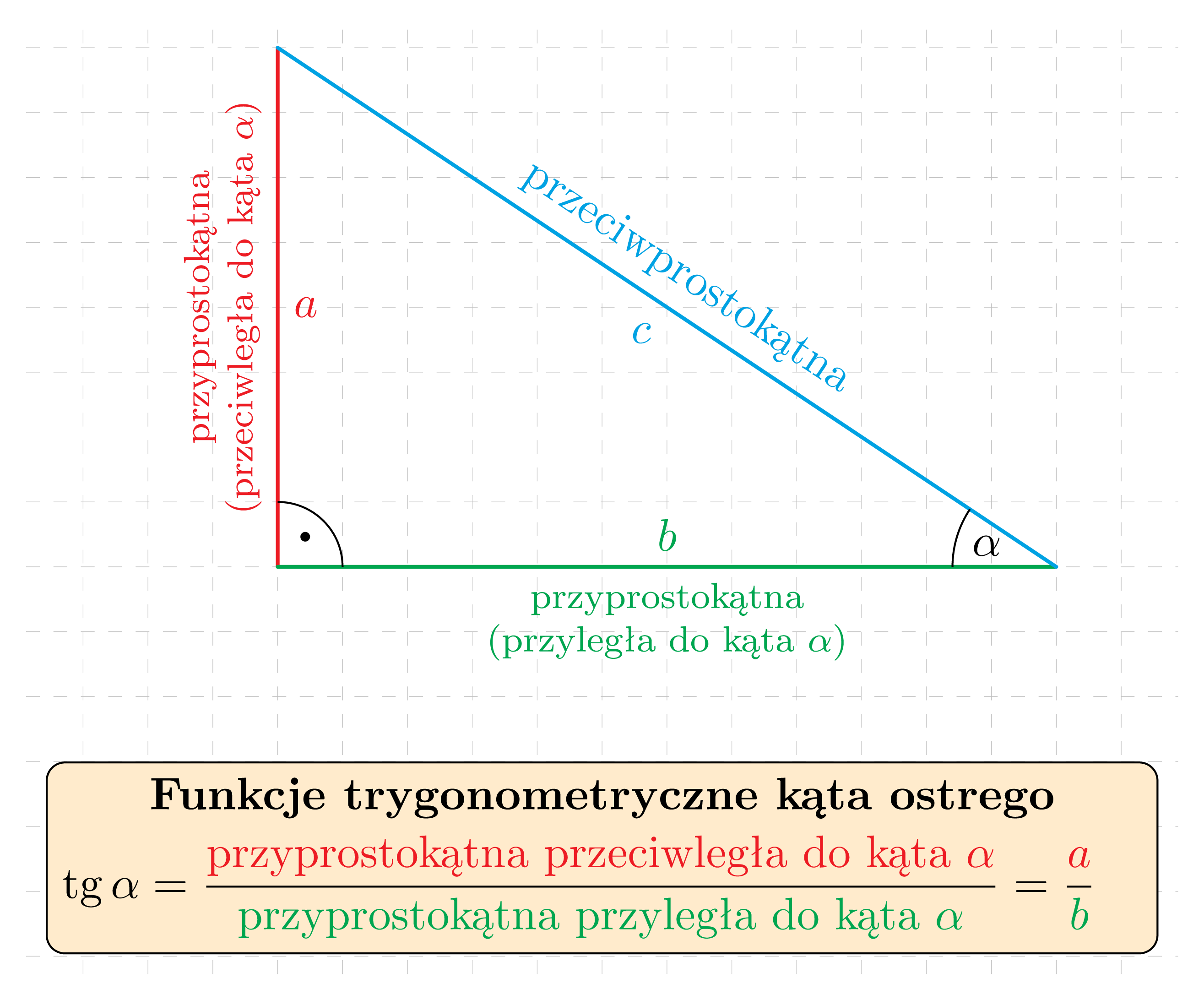
Cotangensem kąta ostrego \alpha w trójkącie prostokątnym nazywamy stosunek długości przyprostokątnej leżącej przy kącie \alpha do długości przyprostokątnej leżącej naprzeciwko kąta \alpha:
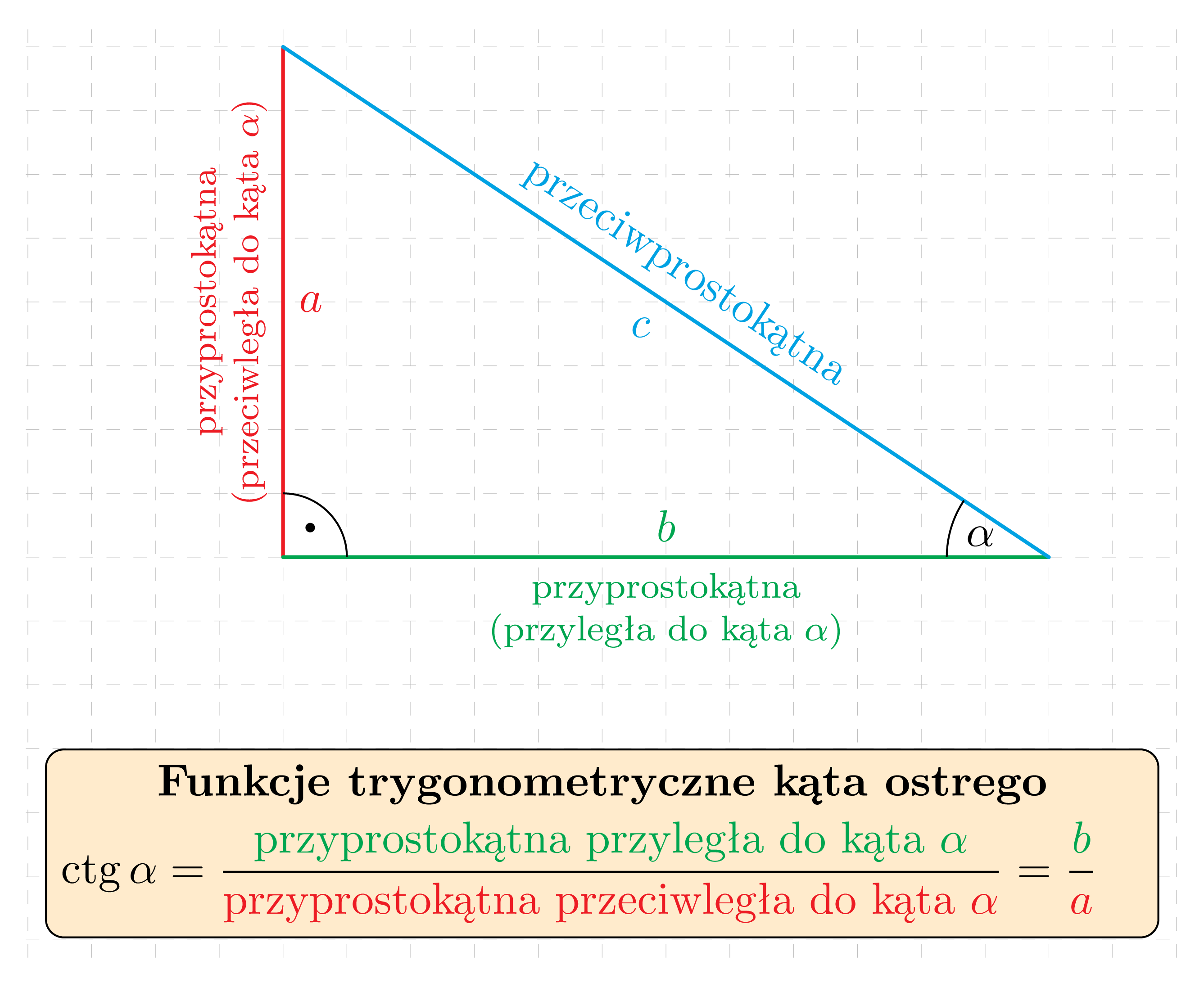

Wprost z definicji funkcji trygonometrycznych kąta ostrego wynika, że \sin\alpha\in(0,1), \cos\alpha\in(0,1), \tg\alpha>0 oraz \ctg\alpha>0.
Jak doskonale wiemy, w trójkątach prostokątnych o kątach 30^\circ ,60^\circ oraz 45^\circ zachodzą specjalne zależności pomiędzy długościami boków, dzięki którym możemy z łatwością wyznaczyć wartości funkcji trygonometrycznych dla tych właśnie kątów. Jeśli zatem będziemy mieć problem z ich zapamiętaniem, możemy je błyskawicznie obliczyć.


Wartości funkcji trygonometrycznych dla wybranych kątów ostrych oraz kąta zerowego i prostego zostały zebrane w poniższej tabeli:
\alpha | 0^\circ | 30^\circ | 45^\circ | 60^\circ | 90^\circ |
\sin\alpha | 0 | \frac{1}{2} | \frac{\sqrt{2}}{2} | \frac{\sqrt{3}}{2} | 1 |
\cos\alpha | 1 | \frac{\sqrt{3}}{2} | \frac{\sqrt{2}}{2} | \frac{1}{2} | 0 |
\tg\alpha | 0 | \frac{\sqrt{3}}{3} | 1 | \sqrt{3} | nie istnieje |
\ctg\alpha | nie istnieje | \sqrt{3} | 1 | \frac{\sqrt{3}}{3} | 0 |
Wartości funkcji trygonometrycznych dla wybranych kątów.
Potęgi funkcji symetrycznych, tj. np. \left(\sin\alpha\right)^{2} zapisujemy bez nawiasu, umieszczając potęgę tuż przy nazwie funkcji trygonometrycznej, tj. \sin^2\alpha.
Dla dowolnego kąta ostrego \alpha zachodzi
Dla dowolnego kąta ostrego \alpha zachodzą następujące zależności:
\sin^2\alpha+\cos^2\alpha=1 (jedynka trygonometryczna)
\displaystyle \tg\alpha=\frac{\sin\alpha}{\cos\alpha}
\displaystyle \ctg\alpha=\frac{\cos\alpha}{\sin\alpha}
\tg\alpha \cdot \ctg\alpha=1
Dla dowolnego kąta ostrego \alpha zachodzą następujące równości:
1+\tg^2\alpha=\frac{1}{\cos^2\alpha}
1+\ctg^2\alpha=\frac{1}{\sin^2\alpha}
Wartości funkcji trygonometrycznych dla kątów ostrych oraz kąta zerowego i prostego, w przybliżeniu do czterech miejsc po przecinku zostały zebrane w poniższej tabeli:
\alpha | \sin\alpha | \cos\alpha | \tg\alpha | \ctg\alpha |
0° | 0 | 1 | 0 | nie istnieje |
1° | 0.0175 | 0.9998 | 0.0175 | 57.29 |
2° | 0.0349 | 0.9994 | 0.0349 | 28.6363 |
3° | 0.0523 | 0.9986 | 0.0524 | 19.0811 |
4° | 0.0698 | 0.9976 | 0.0699 | 14.3007 |
5° | 0.0872 | 0.9962 | 0.0875 | 11.4301 |
6° | 0.1045 | 0.9945 | 0.1051 | 9.5144 |
7° | 0.1219 | 0.9925 | 0.1228 | 8.1443 |
8° | 0.1392 | 0.9903 | 0.1405 | 7.1154 |
9° | 0.1564 | 0.9877 | 0.1584 | 6.3138 |
10° | 0.1736 | 0.9848 | 0.1763 | 5.6713 |
11° | 0.1908 | 0.9816 | 0.1944 | 5.1446 |
12° | 0.2079 | 0.9781 | 0.2126 | 4.7046 |
13° | 0.225 | 0.9744 | 0.2309 | 4.3315 |
14° | 0.2419 | 0.9703 | 0.2493 | 4.0108 |
15° | 0.2588 | 0.9659 | 0.2679 | 3.7321 |
16° | 0.2756 | 0.9613 | 0.2867 | 3.4874 |
17° | 0.2924 | 0.9563 | 0.3057 | 3.2709 |
18° | 0.309 | 0.9511 | 0.3249 | 3.0777 |
19° | 0.3256 | 0.9455 | 0.3443 | 2.9042 |
20° | 0.342 | 0.9397 | 0.364 | 2.7475 |
21° | 0.3584 | 0.9336 | 0.3839 | 2.6051 |
22° | 0.3746 | 0.9272 | 0.404 | 2.4751 |
23° | 0.3907 | 0.9205 | 0.4245 | 2.3559 |
24° | 0.4067 | 0.9135 | 0.4452 | 2.246 |
25° | 0.4226 | 0.9063 | 0.4663 | 2.1445 |
26° | 0.4384 | 0.8988 | 0.4877 | 2.0503 |
27° | 0.454 | 0.891 | 0.5095 | 1.9626 |
28° | 0.4695 | 0.8829 | 0.5317 | 1.8807 |
29° | 0.4848 | 0.8746 | 0.5543 | 1.804 |
30° | 0.5 | 0.866 | 0.5774 | 1.7321 |
31° | 0.515 | 0.8572 | 0.6009 | 1.6643 |
32° | 0.5299 | 0.848 | 0.6249 | 1.6003 |
33° | 0.5446 | 0.8387 | 0.6494 | 1.5399 |
34° | 0.5592 | 0.829 | 0.6745 | 1.4826 |
35° | 0.5736 | 0.8192 | 0.7002 | 1.4281 |
36° | 0.5878 | 0.809 | 0.7265 | 1.3764 |
37° | 0.6018 | 0.7986 | 0.7536 | 1.327 |
38° | 0.6157 | 0.788 | 0.7813 | 1.2799 |
39° | 0.6293 | 0.7771 | 0.8098 | 1.2349 |
40° | 0.6428 | 0.766 | 0.8391 | 1.1918 |
41° | 0.6561 | 0.7547 | 0.8693 | 1.1504 |
42° | 0.6691 | 0.7431 | 0.9004 | 1.1106 |
43° | 0.682 | 0.7314 | 0.9325 | 1.0724 |
44° | 0.6947 | 0.7193 | 0.9657 | 1.0355 |
45° | 0.7071 | 0.7071 | 1 | 1 |
46° | 0.7193 | 0.6947 | 1.0355 | 0.9657 |
47° | 0.7314 | 0.682 | 1.0724 | 0.9325 |
48° | 0.7431 | 0.6691 | 1.1106 | 0.9004 |
49° | 0.7547 | 0.6561 | 1.1504 | 0.8693 |
50° | 0.766 | 0.6428 | 1.1918 | 0.8391 |
51° | 0.7771 | 0.6293 | 1.2349 | 0.8098 |
52° | 0.788 | 0.6157 | 1.2799 | 0.7813 |
53° | 0.7986 | 0.6018 | 1.327 | 0.7536 |
54° | 0.809 | 0.5878 | 1.3764 | 0.7265 |
55° | 0.8192 | 0.5736 | 1.4281 | 0.7002 |
56° | 0.829 | 0.5592 | 1.4826 | 0.6745 |
57° | 0.8387 | 0.5446 | 1.5399 | 0.6494 |
58° | 0.848 | 0.5299 | 1.6003 | 0.6249 |
59° | 0.8572 | 0.515 | 1.6643 | 0.6009 |
60° | 0.866 | 0.5 | 1.7321 | 0.5774 |
61° | 0.8746 | 0.4848 | 1.804 | 0.5543 |
62° | 0.8829 | 0.4695 | 1.8807 | 0.5317 |
63° | 0.891 | 0.454 | 1.9626 | 0.5095 |
64° | 0.8988 | 0.4384 | 2.0503 | 0.4877 |
65° | 0.9063 | 0.4226 | 2.1445 | 0.4663 |
66° | 0.9135 | 0.4067 | 2.246 | 0.4452 |
67° | 0.9205 | 0.3907 | 2.3559 | 0.4245 |
68° | 0.9272 | 0.3746 | 2.4751 | 0.404 |
69° | 0.9336 | 0.3584 | 2.6051 | 0.3839 |
70° | 0.9397 | 0.342 | 2.7475 | 0.364 |
71° | 0.9455 | 0.3256 | 2.9042 | 0.3443 |
72° | 0.9511 | 0.309 | 3.0777 | 0.3249 |
73° | 0.9563 | 0.2924 | 3.2709 | 0.3057 |
74° | 0.9613 | 0.2756 | 3.4874 | 0.2867 |
75° | 0.9659 | 0.2588 | 3.7321 | 0.2679 |
76° | 0.9703 | 0.2419 | 4.0108 | 0.2493 |
77° | 0.9744 | 0.225 | 4.3315 | 0.2309 |
78° | 0.9781 | 0.2079 | 4.7046 | 0.2126 |
79° | 0.9816 | 0.1908 | 5.1446 | 0.1944 |
80° | 0.9848 | 0.1736 | 5.6713 | 0.1763 |
81° | 0.9877 | 0.1564 | 6.3138 | 0.1584 |
82° | 0.9903 | 0.1392 | 7.1154 | 0.1405 |
83° | 0.9925 | 0.1219 | 8.1443 | 0.1228 |
84° | 0.9945 | 0.1045 | 9.5144 | 0.1051 |
85° | 0.9962 | 0.0872 | 11.4301 | 0.0875 |
86° | 0.9976 | 0.0698 | 14.3007 | 0.0699 |
87° | 0.9986 | 0.0523 | 19.0811 | 0.0524 |
88° | 0.9994 | 0.0349 | 28.6363 | 0.0349 |
89° | 0.9998 | 0.0175 | 57.29 | 0.0175 |
90° | 1 | 0 | nie istnieje | 0 |
Wartości funkcji trygonometrycznych kątów ostrych z przybliżeniem do 4 miejsc po przecinku.