MathWizards

Definicja 1

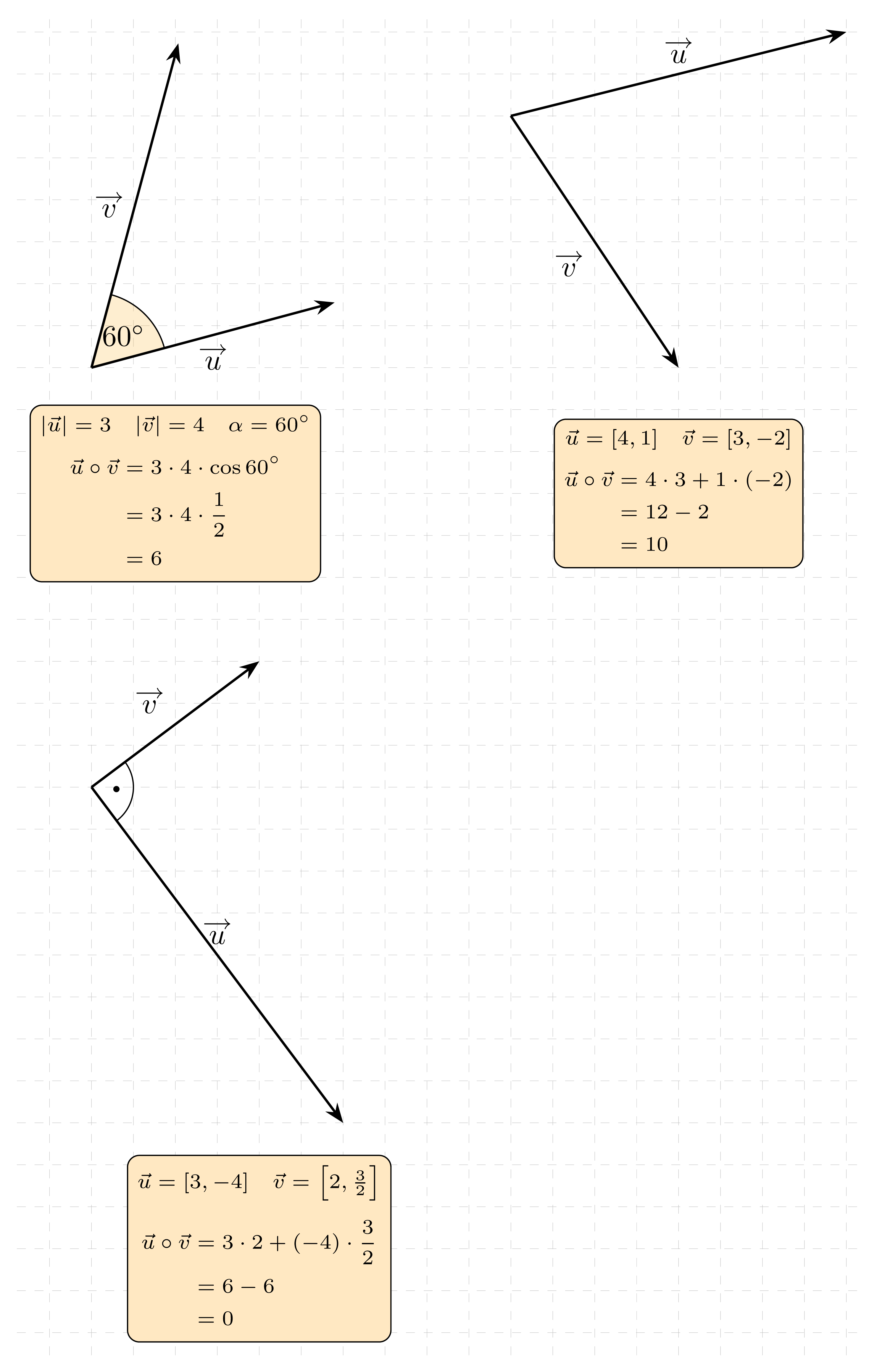
Iloczynem skalarnym wektorów $\vec{u}=[u_x, u_y]$ \vec{u}=[u_x, u_y] oraz $\vec{v}=[v_x, v_y]$ \vec{v}=[v_x, v_y] nazywamy liczbę:

\vec{u}\circ \vec{v}=u_xv_x+u_yv_y

(0)

Równoważnie możemy zapisać:

\vec{u}\circ\vec{v}=|\vec{u}|\cdot |\vec{v}|\cdot \cos \alpha

(0)

Zauważ, że gdy $\alpha=0^\circ$ \alpha=0^\circ , to $\vec{u}\circ \vec{v}=0$ \vec{u}\circ \vec{v}=0, bo $\cos90^\circ =0$ \cos90^\circ =0.

Twierdzenie 1

Dwa wektory są prostopadłe wtedy i tylko wtedy, gdy ich iloczyn skalarny jest równy $0$ 0.

\vec{u}\perp\vec{v}\iff \vec{u}\circ\vec{v}=0

(0)

Przykład 1

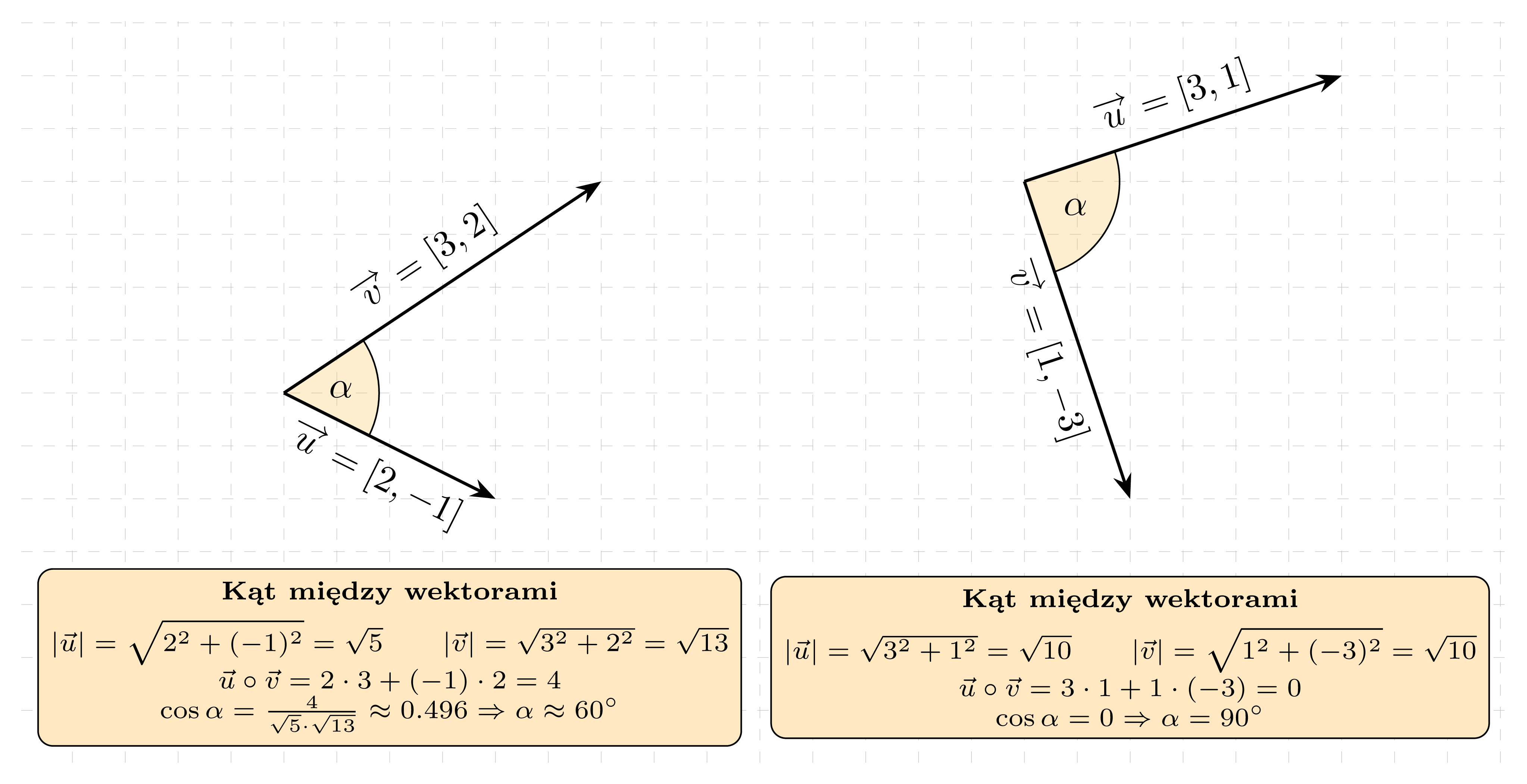
Przekształcając wzór na iloczyn skalarny otrzymujemy wzór na kąt między wektorami:

Twierdzenie 2

Dwa wektory tworzą kąt $\alpha$ \alpha taki że

\begin{aligned} \cos \alpha&=\frac{\vec{u}\circ \vec{v}}{|\vec{u}|\cdot |\vec{v}|} \end{aligned}

(0)

Przykład 2