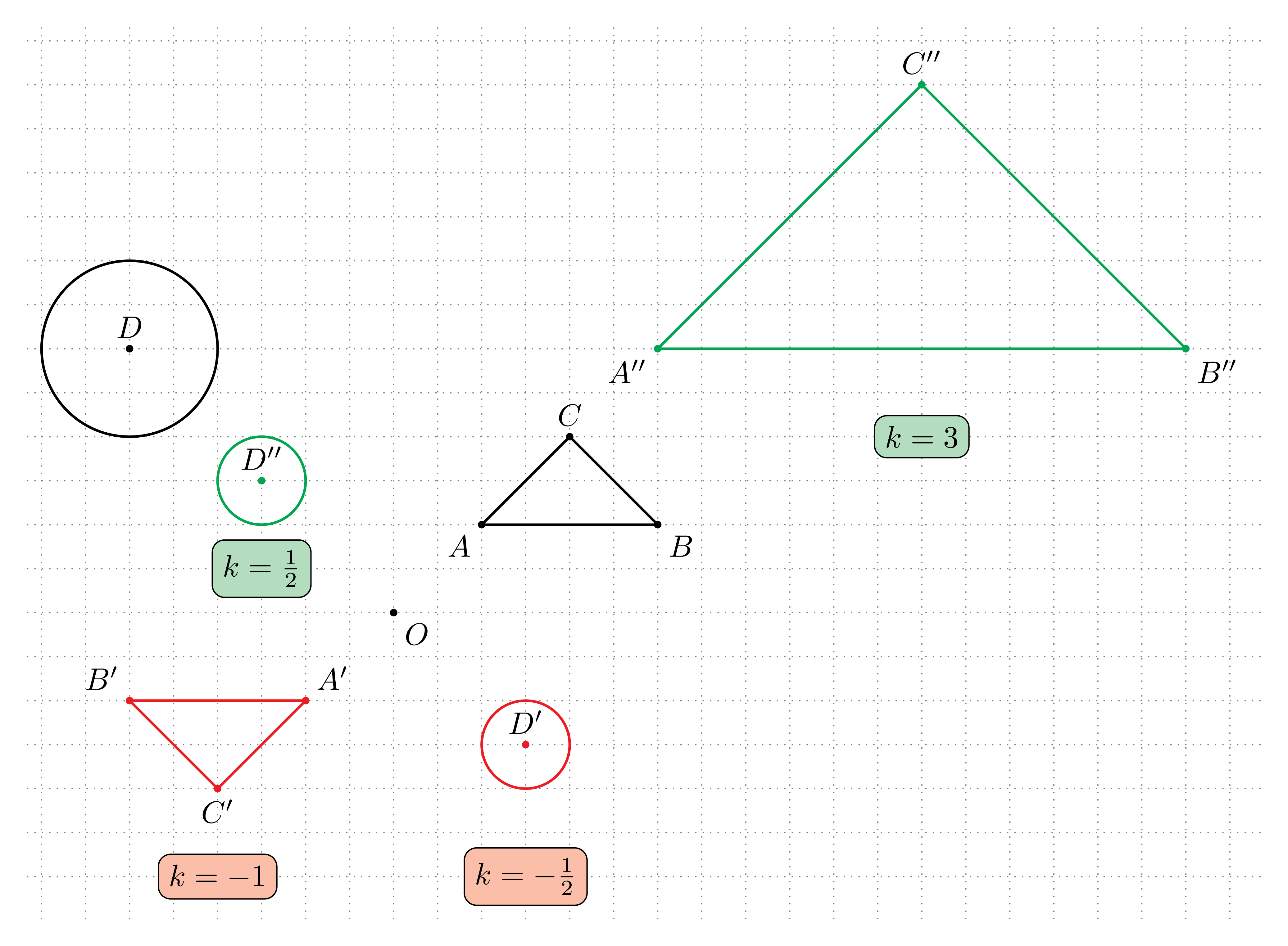
Jednokładność

Jednokładność (inaczej homotetia) to przekształcenie geometryczne, które przekształca każdą figurę na podobną figurę, zachowując proporcje odległości względem pewnego ustalonego środka jednokładności $O$O.

Dla dowolnego punktu $P$P i jego obrazu $P'$P', spełniony jest warunek

gdzie $k$k to skala jednokładności:

• jeżeli $k>1$k>1 - powiększenie figury

• jeżeli $0<k<1$0<k<1 - pomniejszenie figury

• jeżeli $k=1$k=1 - przekształcenie tożsamościowe (brak zmiany)

• $k<0$k<0 - jednokładność z odbiciem (figura zmienia orientację)

W jednokładności o środku $O=\left(x_0,y_0\right)$O=\left(x_0,y_0\right) i skali $k$k zachodzi dla dowolnego punktu $P=\left(x,y\right)$P=\left(x,y\right), jego obraz $P'=\left(x',y'\right)$P'=\left(x',y'\right) ma współrzędne dane wzorami:

Jeśli środek jednokładności to punkt $O=\left(0,0\right)$O=\left(0,0\right), to wzory upraszczają się do:

Oznaczenie: $J_O^k$J_O^k.

W jednokładności o skali $k$k:

• obwód figury zmienia się $|k|$|k| razy

• pole figury zmienia się $k^2$k^2 razy