Liczby rzeczywiste

Liczby rzeczywiste to rozszerzenie liczb wymiernych obejmujące wszystkie możliwe wartości na osi liczbowej, w tym liczby niewymierne.

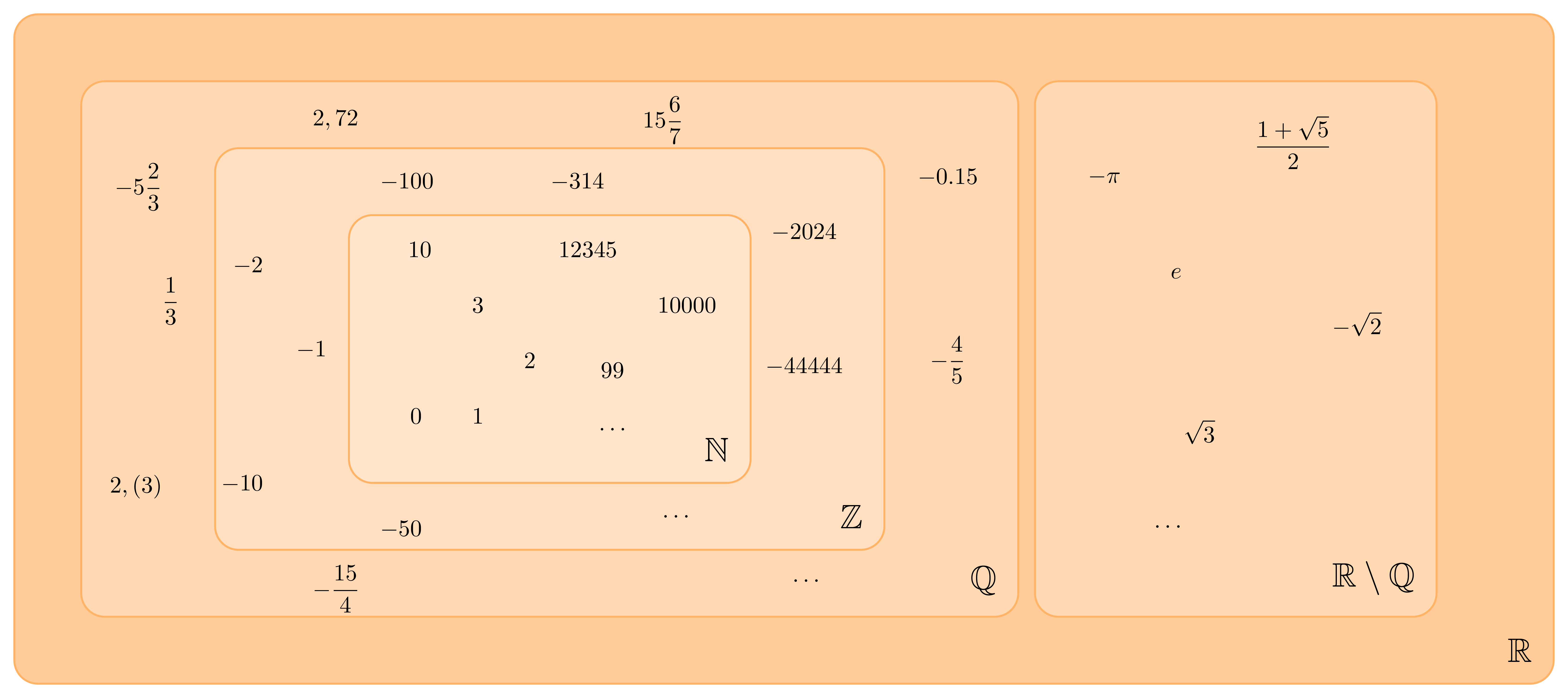
Własności liczb rzeczywistych można utożsamić z własnościami prostej, czyli osi liczbowej na której te liczby są zaznaczane:

• tak jak prosta nie ma początku ani końca, tak w zbiorze liczb rzeczywistych nie ma największej oraz najmniejszej liczby,

• tak jak istnieje nieskończenie wiele punktów między dwoma punktami na prostej, tak istnieje nieskończenie wiele liczb rzeczywistych które leżą pomiędzy dwoma innymi liczbami rzeczywistymi.

• tak jak na prostej punkty są uporządkowane, tak i w zbiorze liczb rzeczywistych dla dwóch różnych liczb $x,y$x,y zachodzi $x<y$x<y lub $x>y$x>y - tj. możemy je porównywać.

W zbiorze liczb rzeczywistych wyróżniamy następujące prawa działań:

• przemienność dodawania - dla dowolnych $x,y\in\mathbb{R}$x,y\in\mathbb{R} zachodzi

  $$x+y=y+x$$

  x+y=y+x(0)

• łączność dodawania - dla dowolnych $x,y,z\in\mathbb{R}$x,y,z\in\mathbb{R} zachodzi:

  $$(x+y)+z=x+(y+z)$$

  (x+y)+z=x+(y+z)(0)

• element neutralny dodawania - dla dowolnego $x\in\mathbb{R}$x\in\mathbb{R} zachodzi:

  $$x+0=x$$

  x+0=x(0)

• element przeciwny - dla dowolnego $x\in\mathbb{R}$x\in\mathbb{R} istnieje liczba przeciwna $(-x)\in\mathbb{R}$(-x)\in\mathbb{R} i zachodzi:

  $$x+(-x)=0$$

  x+(-x)=0(0)

• przemienność mnożenia - dla dowolnych $x,y\in\mathbb{R}$x,y\in\mathbb{R} zachodzi:

  $$x\cdot y=y\cdot x$$

  x\cdot y=y\cdot x(0)

• łączność mnożenia - dla dowolnych $x,y,z\in\mathbb{R}$x,y,z\in\mathbb{R} zachodzi

  $$(x \cdot y) \cdot z=x \cdot (y \cdot z)$$

  (x \cdot y) \cdot z=x \cdot (y \cdot z)(0)

• element neutralny mnożenia - dla dowolnego $x\in\mathbb{R}$x\in\mathbb{R} zachodzi:

  $$x \cdot 1=x$$

  x \cdot 1=x(0)

• element odwrotny - dla dowolnego $x\in\mathbb{R}$x\in\mathbb{R}, $x\neq0$x\neq0, istnieje liczba do niej odwrotna $\displaystyle \frac{1}{x}\in\mathbb{R}$\displaystyle \frac{1}{x}\in\mathbb{R} i zachodzi

  $$x \cdot \frac{1}{x}=1$$

  x \cdot \frac{1}{x}=1 (0)

• rozdzielność mnożenia względem dodawania - dla dowolnych $x,y,z\in\mathbb{R}$x,y,z\in\mathbb{R} zachodzi

  $$x \cdot (y+z)=x \cdot y+x \cdot z$$

  x \cdot (y+z)=x \cdot y+x \cdot z(0)

Odejmowanie i dzielenie nie jest ani łączne, ani przemienne! Jednakże, prawo rozdzielności mnożenia względem odejmowania jest prawdziwe i zachodzi:

Działania w nawiasach → potęgowanie i pierwiastkowanie → mnożenie i dzielenie w kolejności występowania → dodawanie i odejmowani w kolejności występowania.