Okrąg i koło w układzie współrzędnych

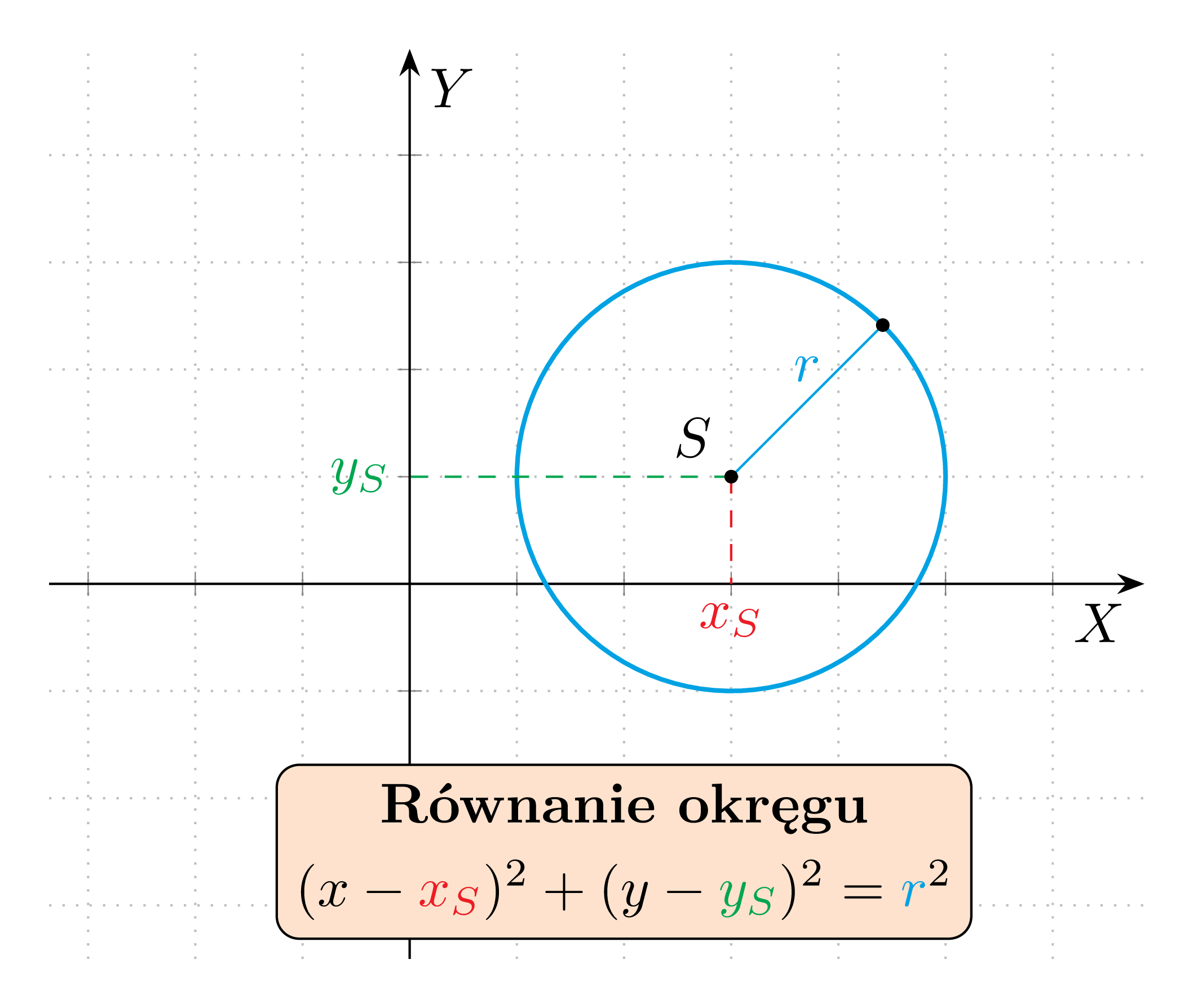
Okrąg o środku w punkcie $(x_S,y_S)$(x_S,y_S) i promieniu $r>0$r>0 jest zbiorem wszystkich punktów płaszczyzny $(x,y)\in\mathbb{R^2}$(x,y)\in\mathbb{R^2} spełniających równanie:

Równanie to nazywamy równaniem okręgu w postaci kanonicznej.

Okrąg może być podany również w postaci ogólnej:

gdzie $c=a^2+b^2-c^2$c=a^2+b^2-c^2

Równaniem okręgu w postaci ogólnej (zredukowanej) o środku w punkcie $\displaystyle S=\left(- \frac{a}{2},- \frac{b}{2} \right)$\displaystyle S=\left(- \frac{a}{2},- \frac{b}{2} \right) i promieniu $\displaystyle r= \frac{a^2+b^2-4c}{2}$\displaystyle r= \frac{a^2+b^2-4c}{2} to równanie postaci:

Koło o środku w punkcie $O=(a,b)$O=(a,b) i promieniu $r>0$r>0 to zbiór punktów płaszczyzny, których współrzędne $(x,y)$(x,y) spełniają nierówność: