Okrąg opisany na czworokącie

Na czworokącie można opisać okrąg wtedy i tylko wtedy, gdy symetralne wszystkich boków tego czworokąta przecinają się w jednym punkcie.

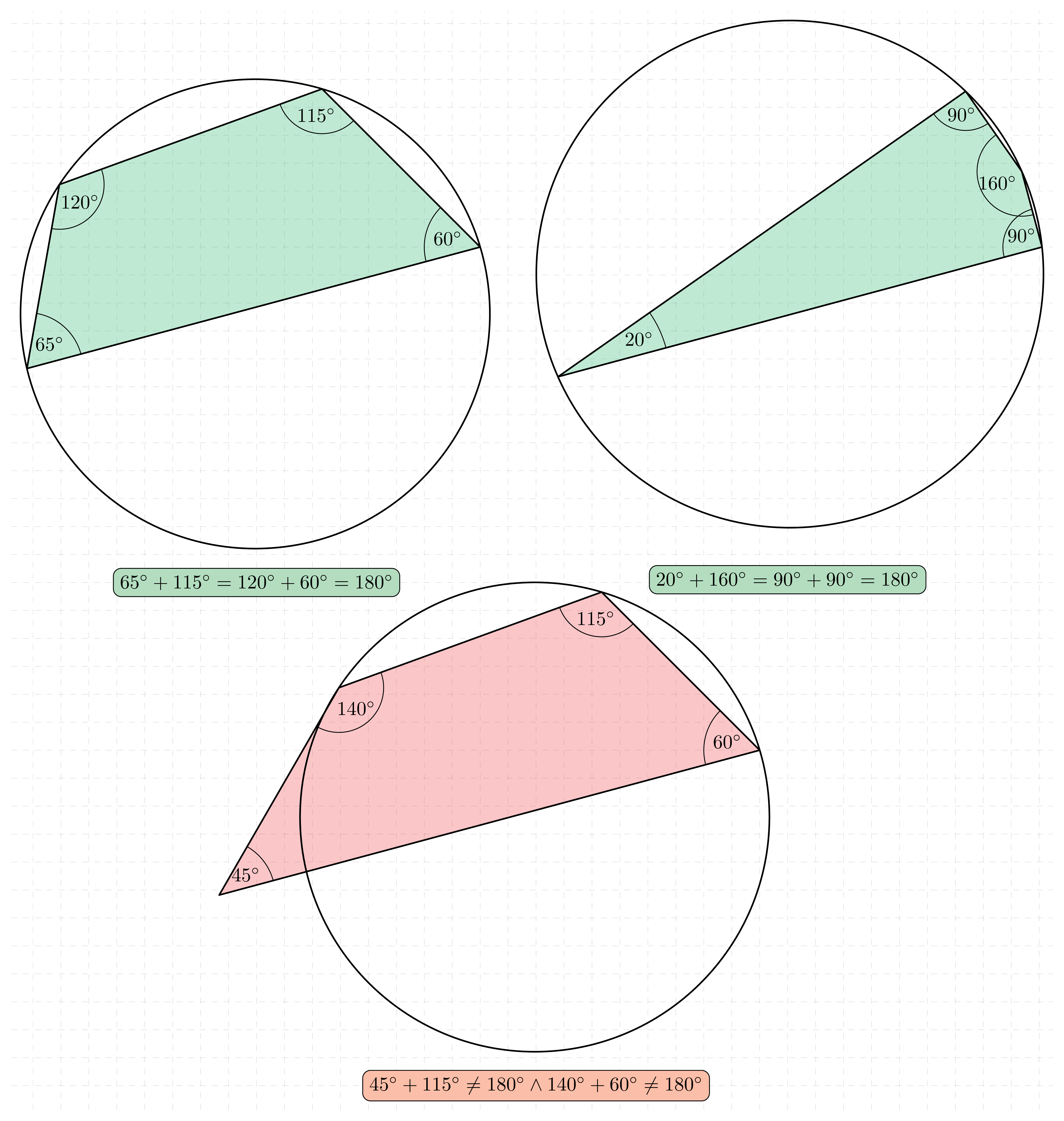
Na czworokącie da się opisać okrąg wtedy i tylko wtedy, gdy sumy miar jego przeciwległych kątów są równe $180^\circ$180^\circ .

Jeżeli na czworokącie o bokach długości $a,b,c,d$a,b,c,d i przekątnych długości $e$e i $f$f da się opisać okrąg, to

Na czworokącie $ABCD$ABCD można opisać okrąg wtedy i tylko wtedy, gdy przekątne $AC$AC i $BD$BD tworzą z bokami odpowiednio $BC$BC i $AD$AD (lub $AD$AD i $BC$BC) kąty tej samej miary, tj. $|\measuredangle ADB|=|\measuredangle ACB|$|\measuredangle ADB|=|\measuredangle ACB| (lub $|\measuredangle CAD|=|\measuredangle CBD|$|\measuredangle CAD|=|\measuredangle CBD|)

Pole czworokąta o bokach długości $a,b,c,d$a,b,c,d na którym da się opisać okrąg wyraża się wzorem:

gdzie

Jeżeli dodatkowo w ten czworokąt da się wpisać okrąg, to

Druga część Twierdzenia wynika z faktu, że jeżeli w czworokąt da się wpisać okrąg, to

Dodatkowo, powyższe Twierdzenie jest szczególnym przypadkiem Twierdzenia Bretschneidera

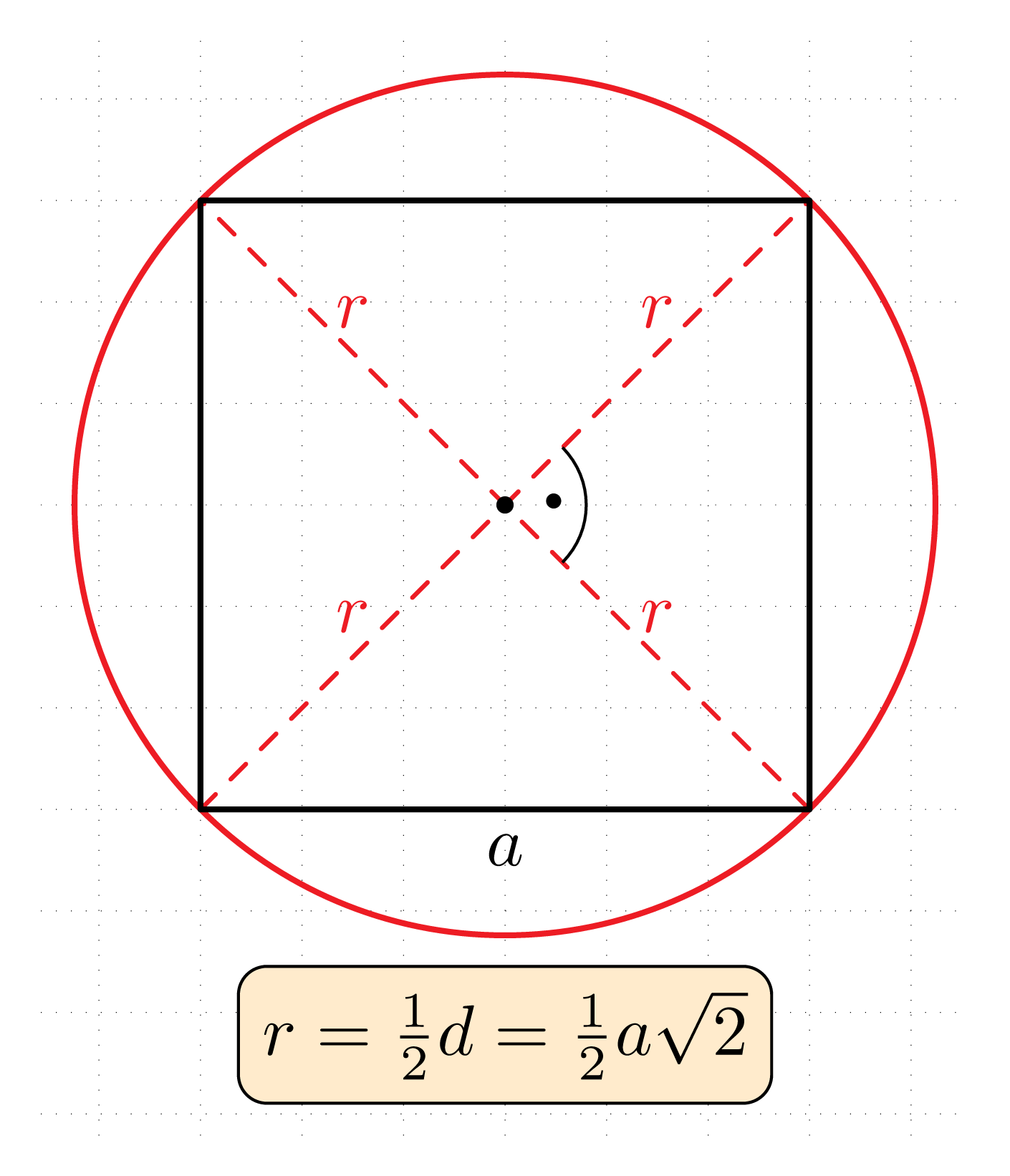
Promień okręgu opisanego na kwadracie o boku długości $a$a jest równy $\frac{a\sqrt{2}}{2}$ \frac{a\sqrt{2}}{2}

Środkiem okręgu opisanego na kwadracie jest punkt przecięcia się przekątnych tego kwadratu. Dodatkowo, promień okręgu jest równy połowie długości przekątnej kwadratu.

Na trapezie można opisać okrąg wtedy i tylko wtedy, gdy jest to trapez równoramienny.