W czworokąt wypukły można wpisać okrąg wtedy i tylko wtedy, gdy dwusieczne wszystkich kątów tego czworokąta przecinają się w jednym punkcie.
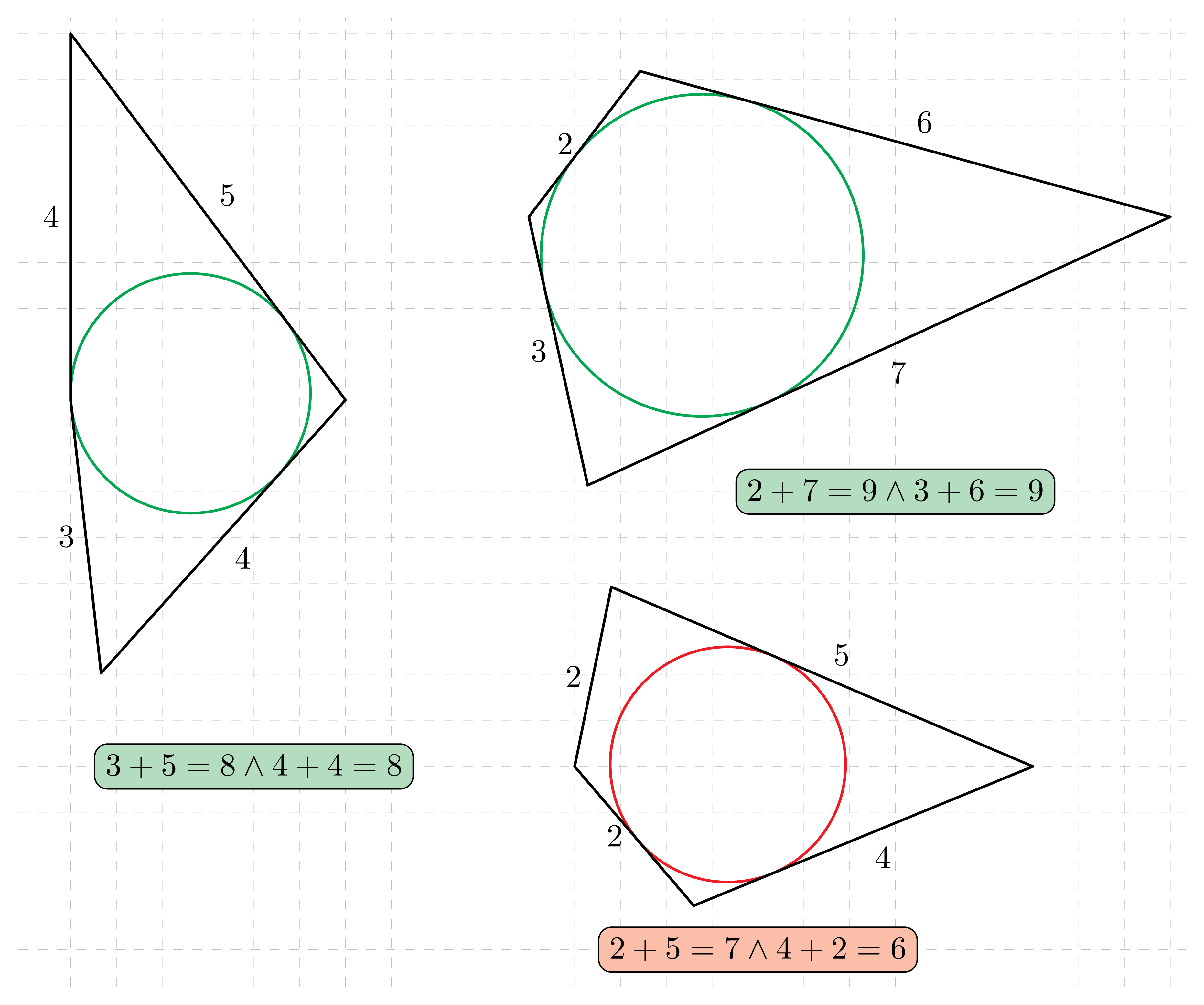
W czworokąt wypukły można wpisać okrąg wtedy i tylko wtedy, gdy sumy długości przeciwległych boków tego czworokąta są równe.
.png)
Pole czworokąta o bokach długości a,b,c,d w który można wpisać okrąg o promieniu r wynosi:
.png)
Uwaga 1
Powyższy wzór wynika z faktu że czworokąt można podzielić na cztery trójkąty o podstawach długości a,b,c,d oraz wysokości r:

Przykład 1
Przykład 2
Promień okręgu wpisanego w kwadrat o boku długości a jest równy \displaystyle \frac{a}{2}
Punkt przecięcia przekątnych jest środkiem okręgu wpisanego w kwadrat
Promień okręgu wpisanego w kwadrat jest równa połowie długości boku tego kwadratu