Ostrosłup

Ostrosłupem nazywamy wielościan, którego jedna ściana, zwana podstawą, jest dowolnym wielokątem, a pozostałe ściany (tzw. ściany boczne) są trójkątami o wspólnym wierzchołku (tzw. wierzchołek ostrosłupa) nieleżącym na płaszczyźnie podstawy. Ostrosłup, którego podstawą jest $n-$n-kąt, nazywamy ostrosłupem $n-$n-kątnym.

Wysokością ostrosłupa nazywamy odcinek (oraz jego długość), którego jednym końcem jest wierzchołek ostrosłupa, a drugim jest rzut prostokątny tego wierzchołka na płaszczyznę podstawy (tzw. spodek wysokości).

Zauważ, że spodek wysokości ostrosłupa pochyłego nie leży na jego podstawie.

Mówimy, że ostrosłup jest prosty, jeżeli jego wszystkie krawędzie boczne są tej samej długości.

Następujące warunki są równoważne:

• ostrosłup jest prosty

• na podstawie tego ostrosłupa można opisać okrąg oraz spodek wysokości tego ostrosłupa jest środkiem okręgu opisanego na jego podstawie,

• wszystkie krawędzie boczne ostrosłupa tworzą jednakowe kąty z płaszczyzną podstawy.

Ostrosłup prosty, który w podstawie ma wielokąt foremny, nazywamy graniastosłupem prawidłowym.

W ostrosłupie prawidłowym, spodek wysokości leży w jednakowych odległościach od wierzchołków podstawy, tj. jest środkiem okręgu opisanego na podstawie tego ostrosłupa.

W szczególności spodek leży:

• trójkąt równoboczny - przecięcie się wysokości trójkąta.

• kwadrat - przecięcie przekątnych podstawy

• pięciokąt foremny - przecięcie się dwusiecznych kątów

Dodatkowo, ściany boczne ostrosłupa prawidłowego są trójkątami równoramiennymi.

Pole powierzchni ostrosłupa wyraża się wzorem:

gdzie $P_p$P_p to pole podstawy ostrosłupa, natomiast $P_b$P_b - suma pól ścian bocznych ostrosłupa.

Objętość dowolnego ostrosłupa dana jest wzorem:

gdzie $P_p$P_p to pole podstawy ostrosłupa, natomiast $H$H - jego wysokością.

Czworościanem foremnym nazywamy ostrosłup prawidłowy trójkątny, tj. ostrosłup którego podstawą oraz ścianami bocznymi są trójkąty równoboczne.

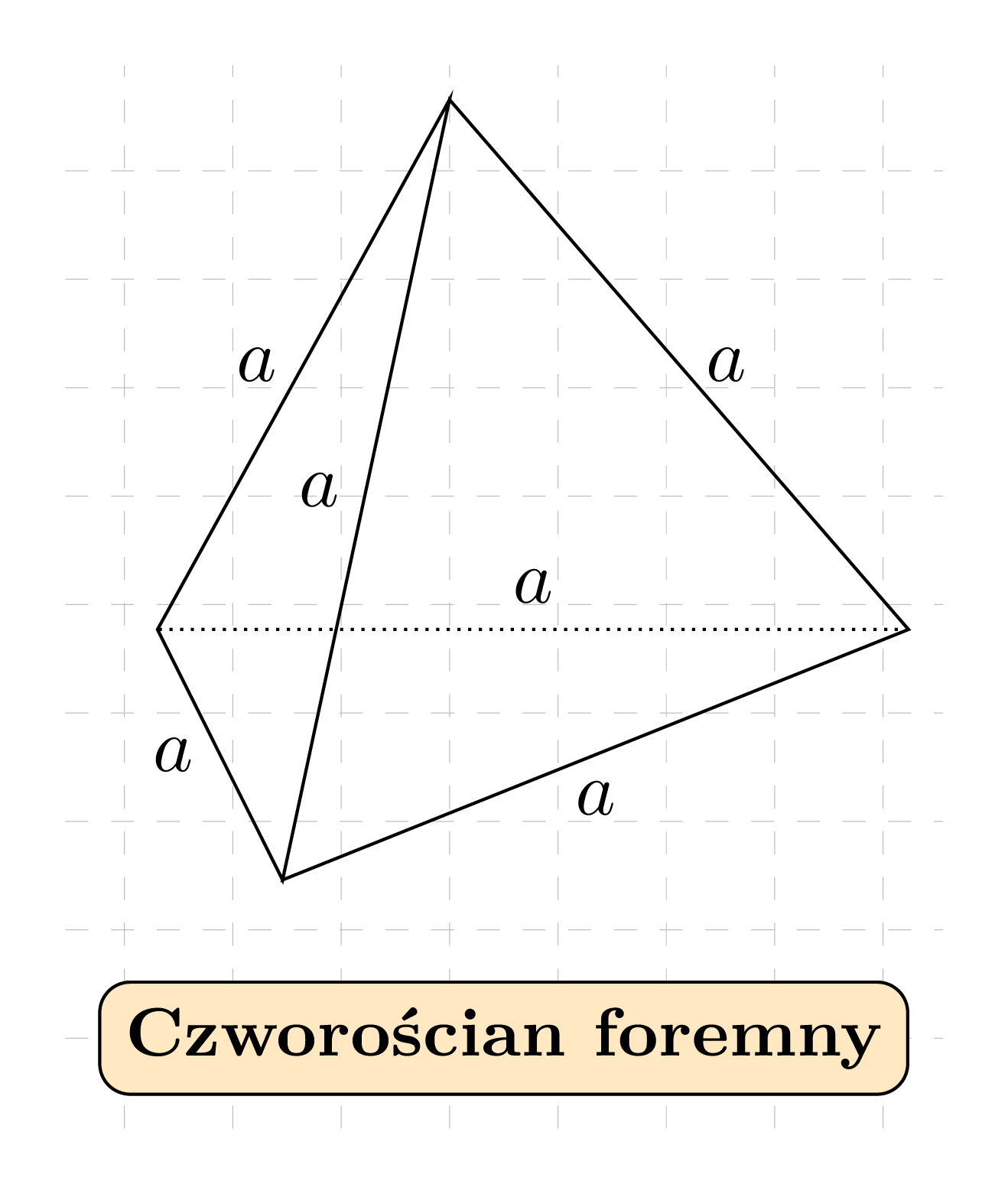
Niech dany będzie czworościan foremny o krawędzi długości $a$a. Wówczas:

Kąt płaski przy wierzchołku ostrosłupa prawidłowego to kąt wyznaczony przez ramiona trójkąta równoramiennego, który tworzy ścianę boczną tego ostrosłupa.

Niech dany będzie ostrosłup prawidłowy czworokątny o wysokości $H$H, wysokości ściany bocznej $h$h oraz długości boku podstawy $a$a. Wówczas:

Niech dany będzie ostrosłup prawidłowy trójkątny o wysokości $H$H, wysokości ściany bocznej $h$h oraz długości boku podstawy $a$a. Wówczas:

Ostrosłup którego podstawą jest $n-$n-kąt posiada:

• $n$n ścian bocznych,

• $n+1$n+1 wszystkich ścian,

• $n+1$n+1 wierzchołków,

• $2n$2n krawędzi

Spodkiem wysokości ostrosłupa prawidłowego trójkątnego jest ortocentrum, czyli punkt przecięcia się wysokości podstawy.