Prosta, półprosta, odcinek, punkt

Punkt to podstawowy obiekt w geometrii, który nie ma wymiarów (tj. nie ma długości, szerokości ani wysokości). W układzie współrzędnych jest określony przez parę liczb $\left(x,y\right)$\left(x,y\right) w przestrzeni $\mathbb{R}^2$\mathbb{R}^2. Punkt oznaczamy wielkimi literami $A,B,C,\ldots$A,B,C,\ldots. i najczęściej zaznaczamy za pomocą kropki (rzadziej za pomocą krzyżyka).

Odcinek to część prostej ograniczona dwoma punktami, zwanymi końcami odcinka. Odcinek zawiera wszystkie punkty leżące między tymi dwoma punktami.

Końce odcinka oznaczamy kreseczkami lub kropkami, a długość odcinka $AB$AB oznaczamy $|AB|$|AB|.

Prosta to zbiór punktów w przestrzeni, który jest jednowymiarowy i nieskończony w obu kierunkach.

Proste oznaczamy małymi literami lub za pomocą liter dwóch punktów leżących na tej prostej. Prosta nie ma początku ani końca.

Mówimy, że dwa lub więcej punktów są współliniowe, jeżeli leżą na tej samej prostej.

Aby odpowiedzieć na pytanie czy dane punkty $A,B,C$A,B,C są współliniowe, należy sprawdzić czy suma długości dwóch odcinków wyznaczonych przez te punkty jest równa długości trzeciego odcinka.

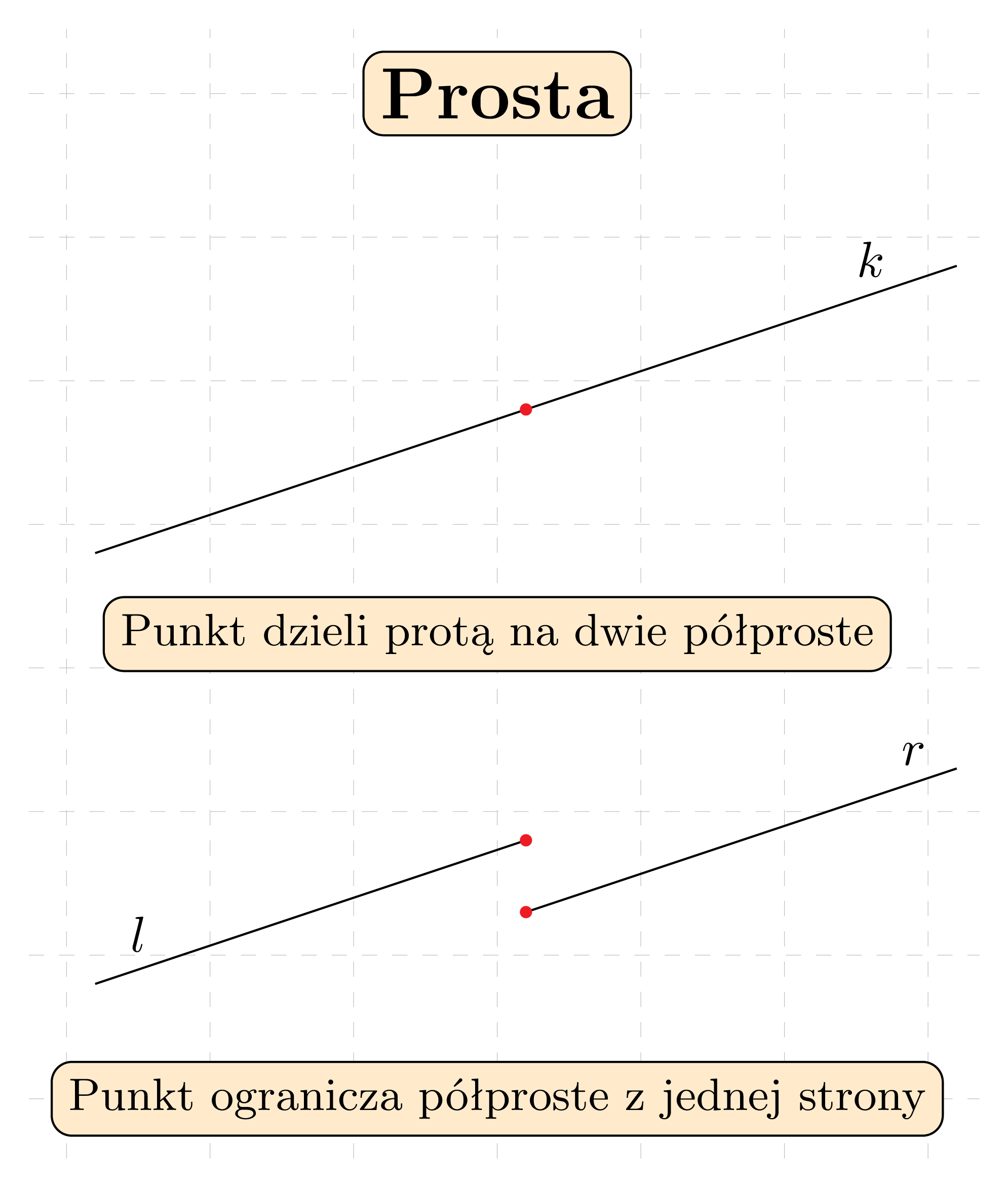
Półprosta to część prostej, która ma jeden punkt początkowy (zwany początkiem półprostej) i rozciąga się nieskończenie w jednym kierunku (składa się z wszystkich punktów tej prostej po jednej ze stron punktu początkowego).

Półprostą oznaczamy małą literą lub za pomocą dwóch punktów z których pierwszy jest początkiem półprostej a drugi jest dowolnym innym punktem który leży na tej półprostej.

Jeżeli dwie półproste o wspólnym początku tworzą jedną prostą, to mówimy że te półproste się dopełniają.

Łamana to skończony ciąg odcinków (nazywanych bokami łamanej), w którym każdy kolejny odcinek zaczyna się w punkcie końcowym poprzedniego. Punkty, w których łączą się kolejne odcinki, nazywane są wierzchołkami łamanej.
Jeżeli początek łamanej pokrywa się z jej końcem (czyli pierwszy i ostatni wierzchołek są tym samym punktem) to łamaną nazywamy zamkniętą, a jeśli nie - otwartą. Dodatkowo, jeżeli odcinki łamanej nie przecinają się (nie mają punktów wspólnych poza wierzchołkami), to łamaną nazywamy zwyczajną, a jeśli mają - wiązaną.

Warto mieć na uwadze, że rysując proste oraz półproste przedstawiamy jedynie ich fragment, ponieważ figury te nie mają początku (prosta) ani końca (prosta i półprosta), czyli są nieograniczone.

Jeżeli trzy różne punkty leżą na jednej prostej, półprostej lub odcinku, to zawsze jeden z nich leży pomiędzy pozostałymi dwoma.

Odległość punktu $P$P od prostej $k$k ($P\notin k$P\notin k) to najmniejsza spośród odległości pomiędzy punktem $P$P i punktami prostej $k$k (lub inaczej: długość najkrótszego odcinka łączącego punkt $P$P z prostą $k$k - odcinek ten jest prostopadły do tej prostej). Oznaczenie: $d(P,k)$d(P,k) i jeżeli $P\in k$P\in k, to $d(P,k)=0$d(P,k)=0.

Najkrótszy odcinek łączący punkt $P$P z prostą $k$k jest do niej prostopadły.

Symetralna odcinka to prosta prostopadła do tego odcinka, przechodząca przez jego środek.

Symetralna odcinka jest zbiorem punktów równo oddalonych od obu końców odcinka.