Przedziały

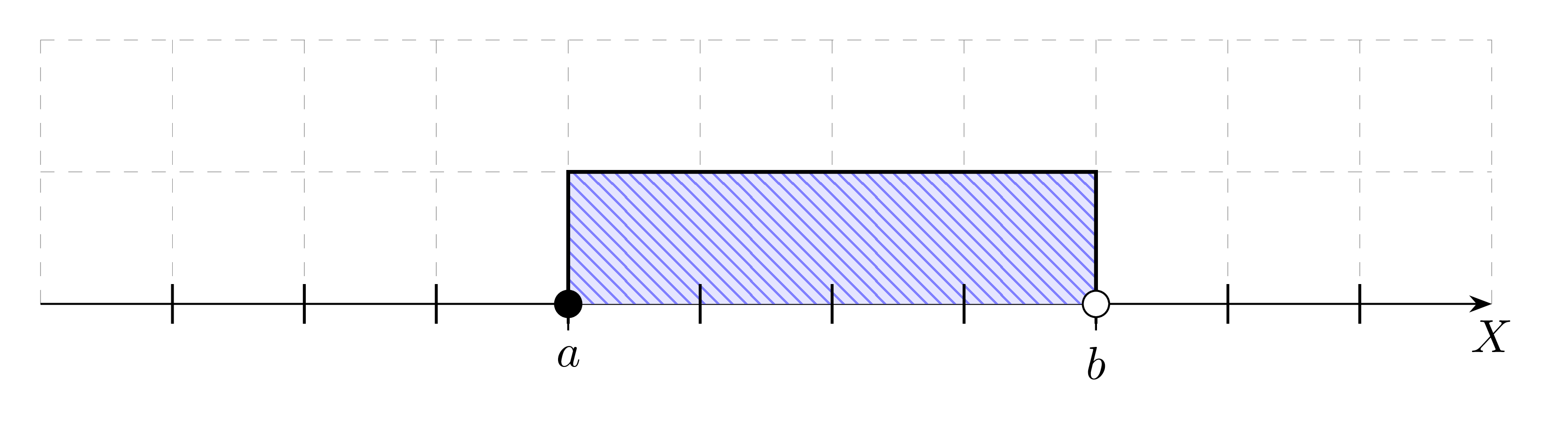
Przedziałem otwartym (obustronnie otwartym) od $a$a do $b$b $(a,b\in\mathbb{R},a<b)$(a,b\in\mathbb{R},a<b) nazywamy zbiór liczb liczb rzeczywistych większych od $a$a i jednocześnie mniejszych od $b$b. Zapisujemy:

Liczby $a$a i $b$b nazywamy końcami przedziału (odpowiednio lewym oraz prawym).

Przedziałem domkniętym (obustronnie domkniętym) od $a$a do $b$b $(a,b\in\mathbb{R},a<b)$(a,b\in\mathbb{R},a<b) nazywamy zbiór liczb rzeczywistych większych bądź równych $a$a oraz jednocześnie mniejszych bądź równych $b$b. Zapisujemy:

Jeśli do przedziału należy tylko jego lewy koniec, to mówimy o przedziale lewostronnie domkniętym, a jeśli do przedziału należy tylko jego prawy koniec to mówimy o przedziale prawostronnie domkniętym. Zapisujemy odpowiednio:

Niech $a\in\mathbb{R}$a\in\mathbb{R}. Przedziałami nieograniczonymi nazywamy następujące przedziały:

• Przedział prawostronnie otwarty nieograniczony - zbiór liczb mniejszych od $a$a:

  $$(-\infty, a)=\{x: x<a\}$$

  (-\infty, a)=\{x: x<a\}(0)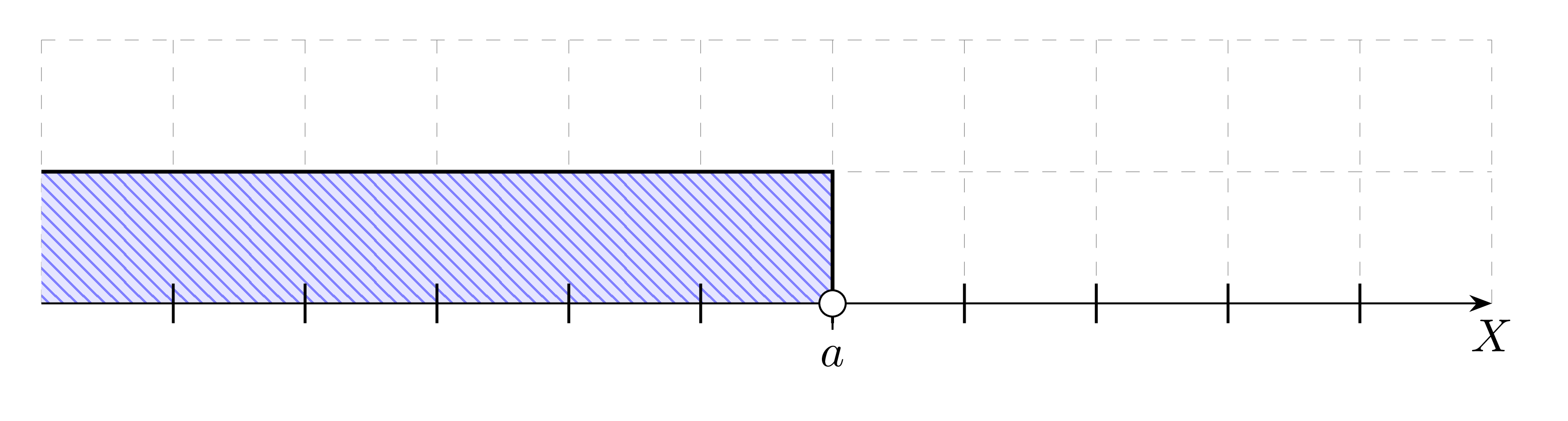
  

• Przedział prawostronnie domknięty nieograniczony - zbiór liczb mniejszych bądź równych $a$a:

  $$(-\infty, a]=\{x: x\le a\}$$

  (-\infty, a]=\{x: x\le a\}(0)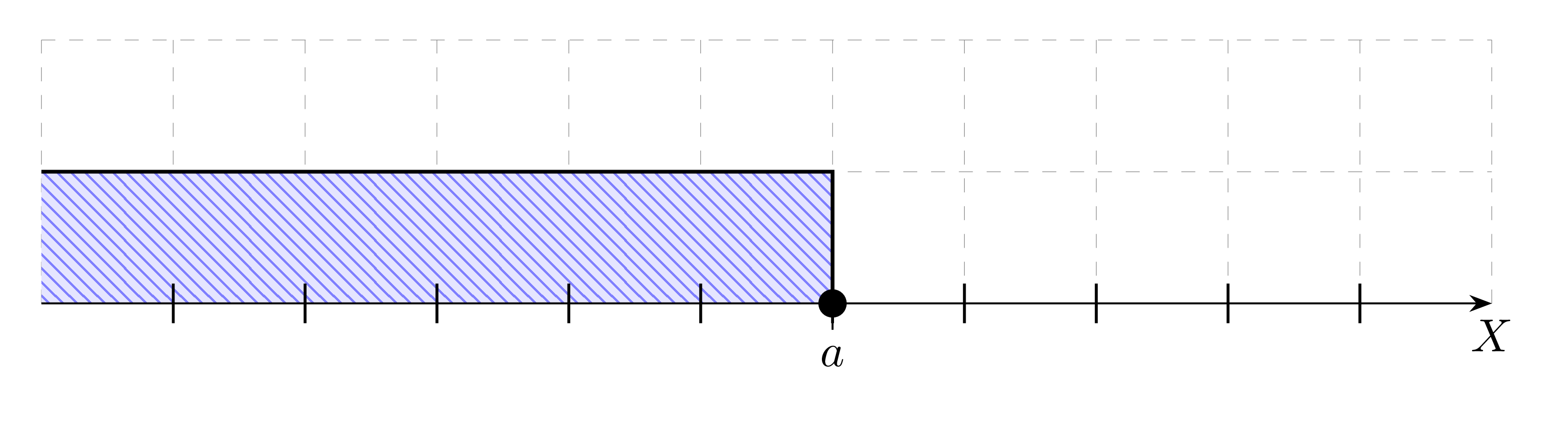
  

• Przedział lewostronnie otwarty nieograniczony - zbiór liczb większych od $a$a:

  $$(a,+\infty)=\{x: x>a\}\\$$

  (a,+\infty)=\{x: x>a\}\\(0)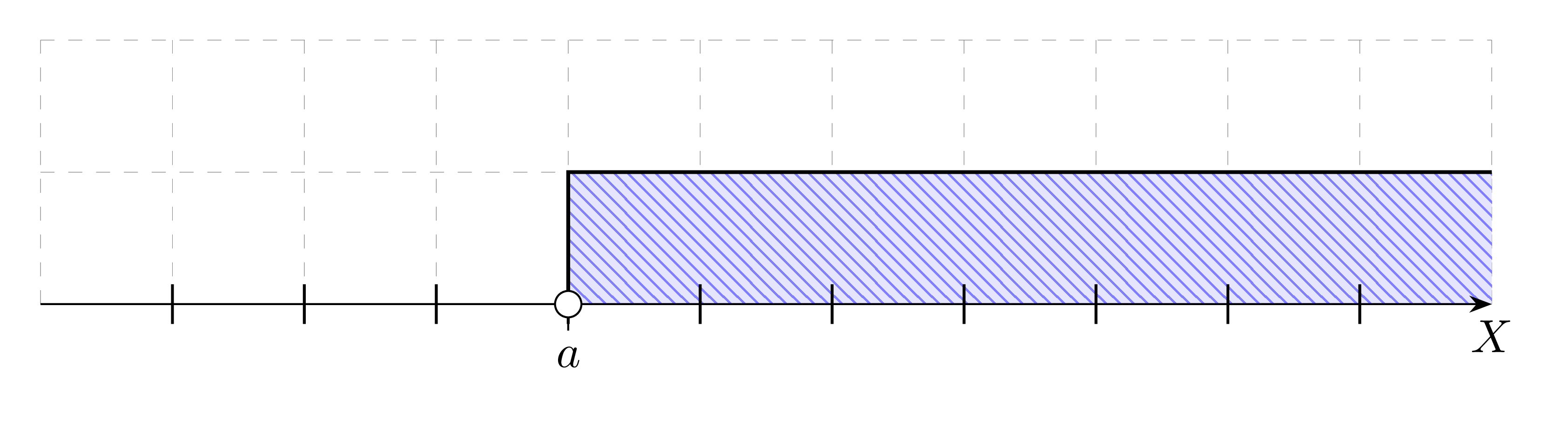
  

• Przedział lewostronnie domknięty nieograniczony - zbiór liczb większych bądź równych $a$a:

  $$[a,+\infty]=\{x: x\ge a\}$$

  [a,+\infty]=\{x: x\ge a\}(0)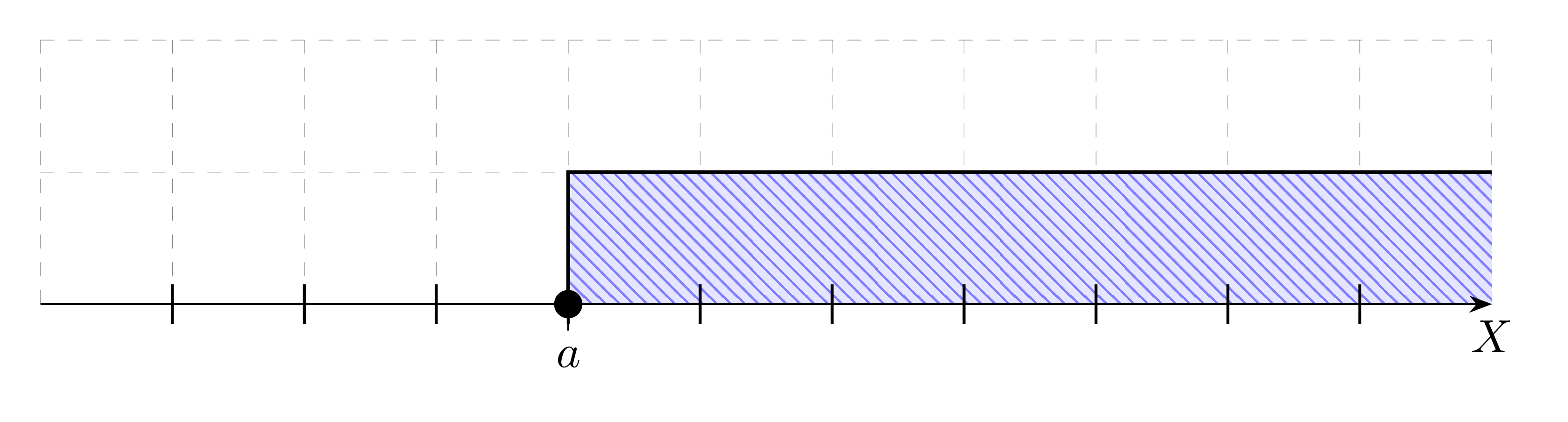
  

• Przedział obustronnie nieograniczony - zbiór liczb rzeczywistych:

  $$(-\infty,\infty)=\{x:x\in\mathbb{R}\}=\mathbb{R}$$

  (-\infty,\infty)=\{x:x\in\mathbb{R}\}=\mathbb{R}(0)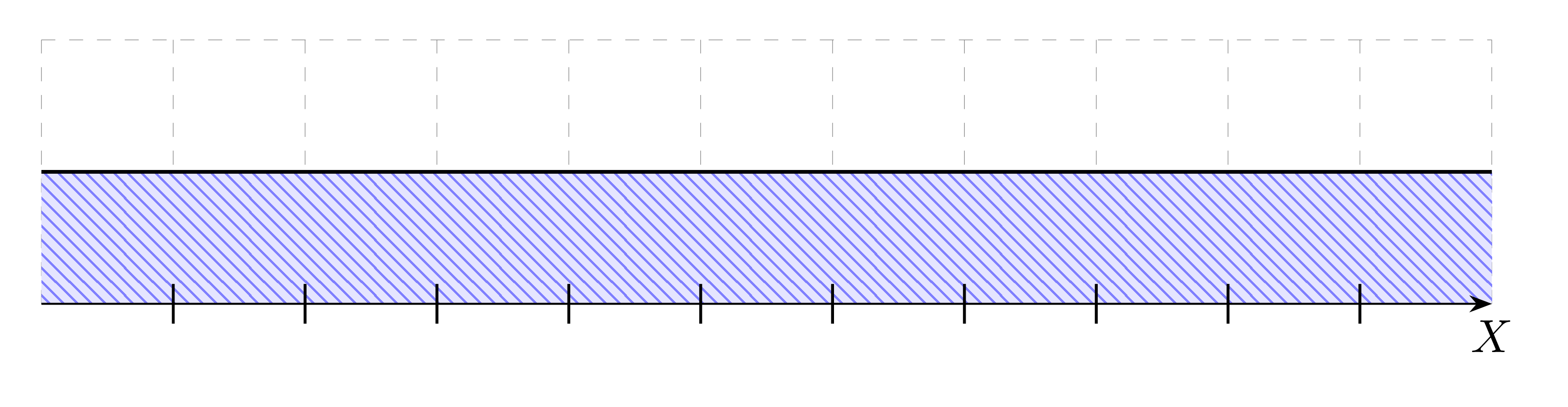
  

Ograniczoność przedziału $(a,b)$(a,b) nie oznacza że jest to zbiór skończony (ma skończoną liczbę elementów). Wręcz przeciwnie, jeśli $a<b$a<b to każdy przedział $(a,b)$(a,b) zawiera nieskończoną liczbę elementów, ponieważ istnieje nieskończenie wiele liczb rzeczywistych pomiędzy $a$a i $b$b.

Zauważ, że $a\notin(a,b)$a\notin(a,b) oraz $b\notin(a,b)$b\notin(a,b). Z drugiej natomiast strony, $a\in[a,b]$a\in[a,b] oraz $b\in[a,b]$b\in[a,b]. W przypadku zbiorów jednostronnie domkniętych: $a\in[a,b)$a\in[a,b) oraz $b\notin[a,b)$b\notin[a,b) i $a\notin(a,b]$a\notin(a,b] oraz $b\in(a,b]$b\in(a,b].
Analogicznie: $a\notin(a,\infty)$a\notin(a,\infty) oraz $a\notin (-\infty,a)$a\notin (-\infty,a) i $a\in[a,\infty)$a\in[a,\infty) oraz $a\in(-\infty,a]$a\in(-\infty,a].

Zauważ, że przedziały lewostronnie oraz prawostronnie domknięte możemy równoważnie nazwać odpowiednio przedziałami prawostronnie oraz lewostronnie otwartymi.

Fakt, że punkt nie należy do danego przedziału oznaczamy na rysunku niezamalowanym kółkiem, a jeśli należy - zamalowanym.

W przedziale otwartym nie ma ani liczby największej, ani najmniejszej. W przedziale lewostronnie otwartym nie ma liczby najmniejszej, a w prawostronnie otwartym - największej.