Rombem (“kopniętym kwadratem”) nazywamy czworokąt mający wszystkie boki równe.

Każdy kwadrat jest rombem, ale nie każdy romb jest kwadratem!
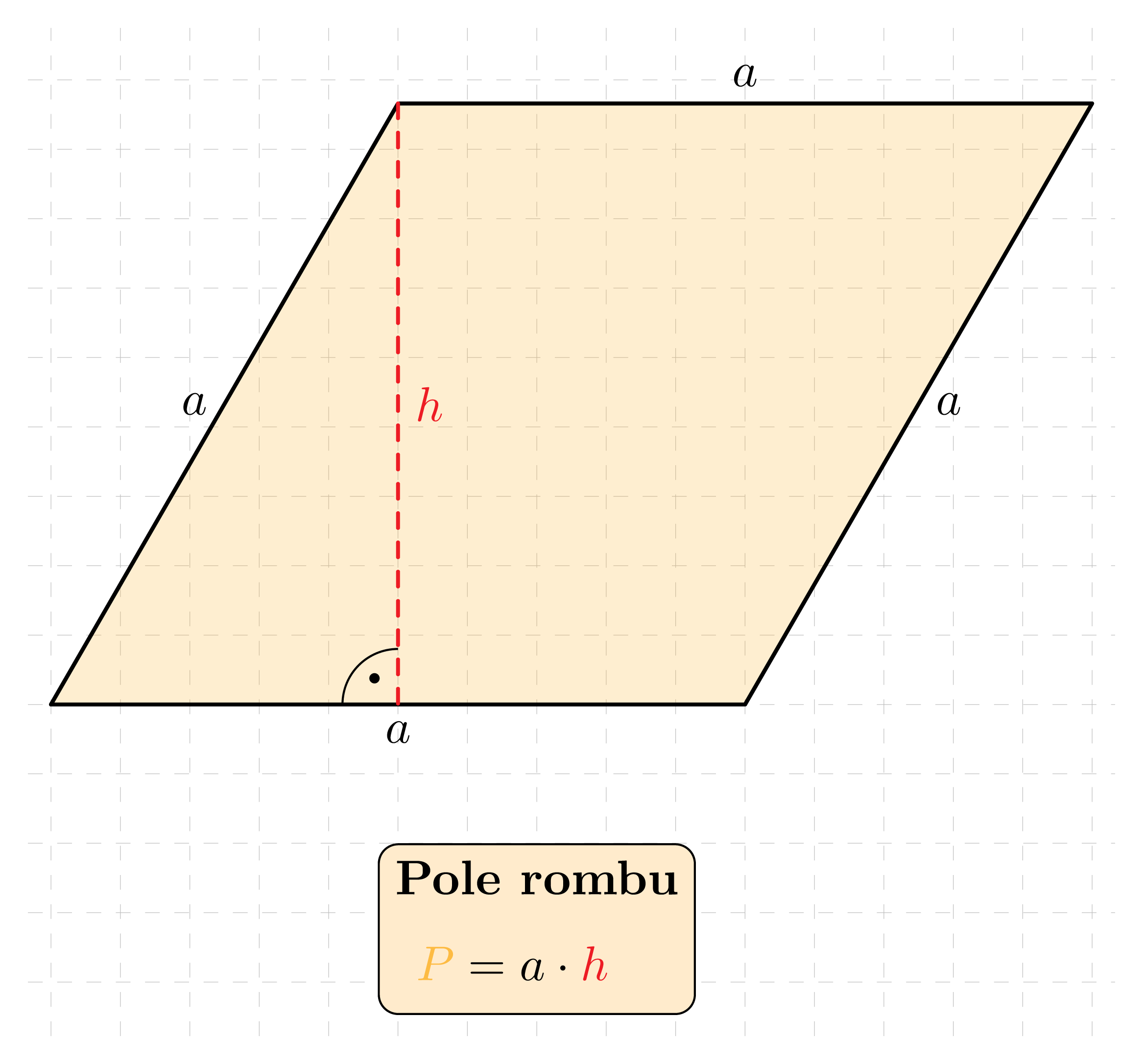
Ponieważ romb jest również równoległobokiem, jego pole możemy obliczyć ze wzoru P=a\cdot h, gdzie a to bok równoległoboku a h - wysokość. Alternatywnie, pole rombu możemy wyrazić przy pomocy długości jego przekątnych korzystając ze wzoru
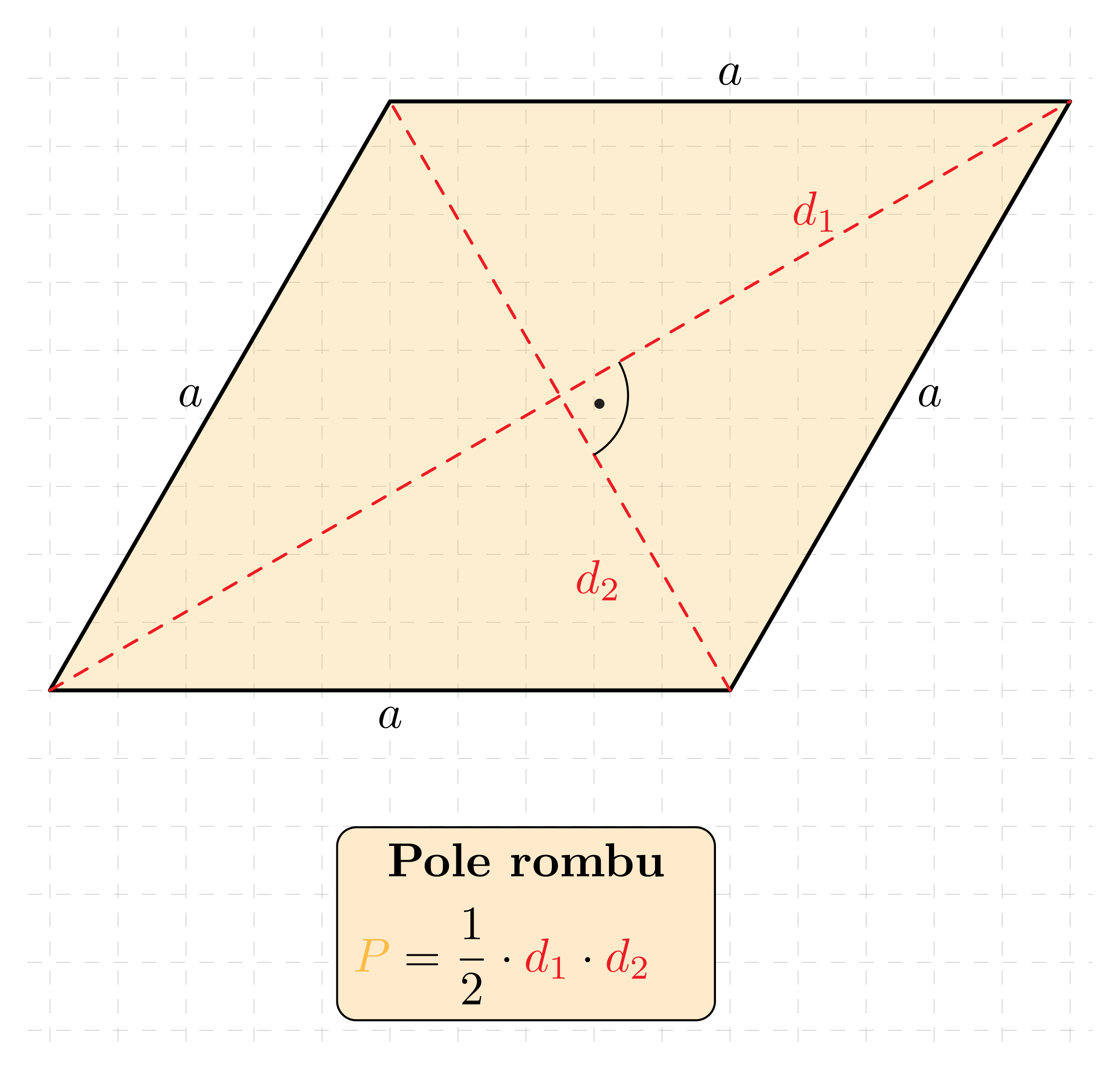
Wzór ten wynika z prostego faktu, że z dwóch rombów można ułożyć prostokąt o bokach długości e i f, a ponieważ jego pole wynosi e \cdot f, to pole jednego rombu musi wynosić \displaystyle \frac{e \cdot f}{2} .

Pole rombu o boku długości a oraz wysokości h dane jest wzorem:
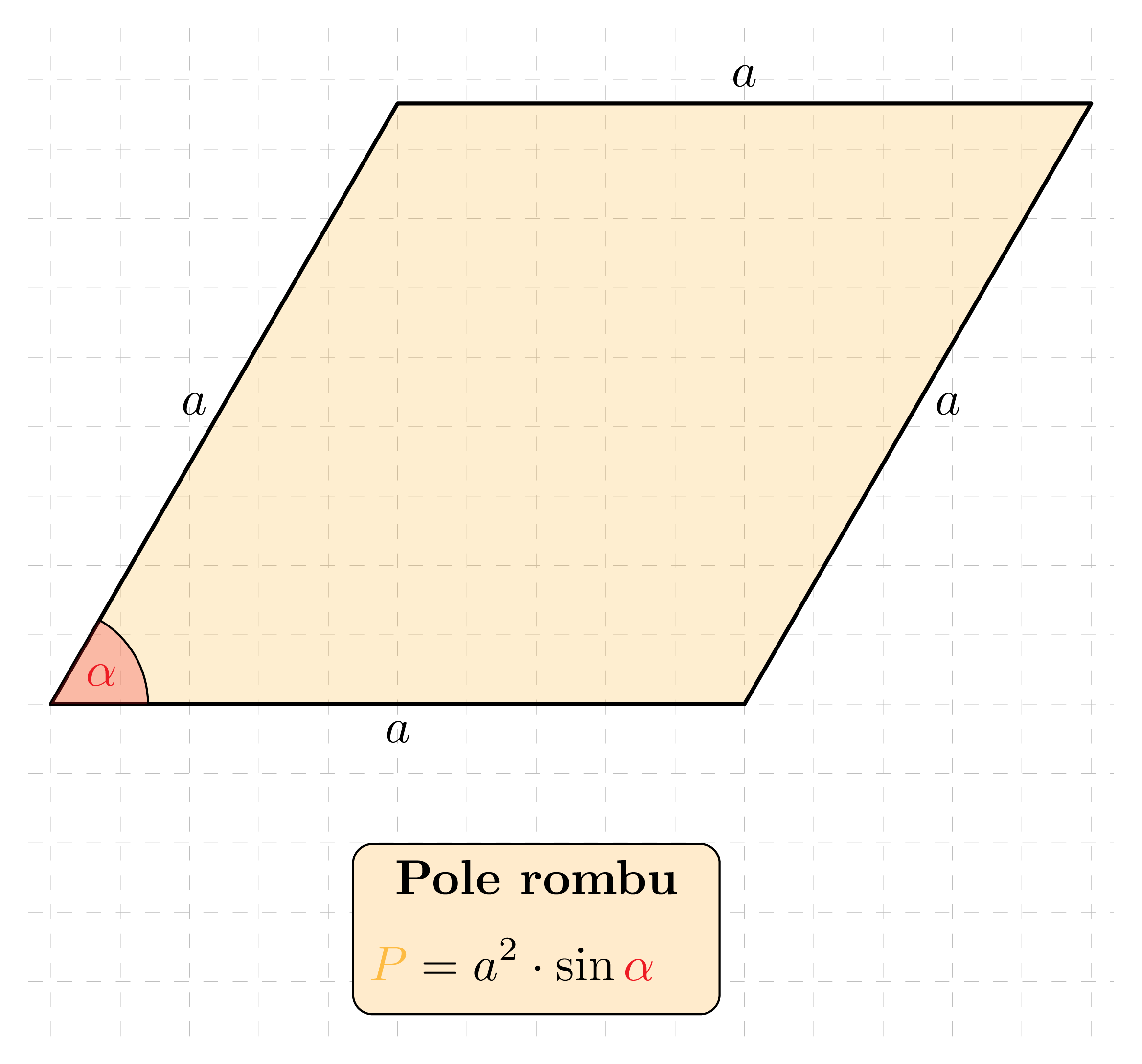
Pole rombu o boku długości a oraz kącie ostrym \alpha wyraża się wzorem:
Pole rombu o przekątnych długości d_1 i d_2 wyraża się wzorem:
Pole rombu o boku długości a i promieniu r okręgu wpisanego w ten romb wyraża się wzorem:


Przekątne rombu przecinają się w połowie, są prostopadłe i leżą na dwusiecznych kątów tego rombu.
.png)
Kąty znajdujące się w przeciwległych wierzchołkach rombu mają równe miary, a suma miar kątów leżących przy tym samym boku wynosi 180^\circ .

Przekątne rombu dzielą ten romb na dwa przystające trójkąty równoramienne.
Jeżeli czworokąt spełnia chociaż jeden z poniższych warunków, to czworokąt ten jest rombem:
wszystkie boki są równej długości,
jest równoległobokiem którego przekątne leżą na dwusiecznych jego kątów
jest równoległobokiem którego przekątne przecinają się pod kątem prostym