Równoległobokiem (“kopniętym prostokątem”) nazywamy czworokąt który ma dwie pary boków równoległych.

Każdy prostokąt (i kwadrat) jest równoległobokiem, ale nie każdy równoległobok jest prostokątem (lub kwadratem)!
Wysokością równoległoboku nazywamy każdy odcinek łączący równoległe boki równoległoboku (lub ich przedłużenia) i będący do nich prostopadły.

Podstawą równoległoboku nazywamy bok równoległoboku do którego została poprowadzona wysokość z wierzchołka równoległoboku.

Wysokością równoległoboku nazywamy również długość odcinka z powyższej definicji. Dodatkowo, ponieważ równoległobok ma dwie pary boków równoległych, to może mieć dwie różne wysokości.
Zauważ, że jeżeli równoległobok o podstawie a i wysokości h przetniemy na dwie części wzdłuż wzdłuż wysokości h, to możemy złożyć z nich prostokąt o bokach długości a i h. Pole równoległoboku jest zatem równe polu tego prostokąta i wynosi P=a \cdot h.

Pole równoległoboku o bokach długości a i b oraz wysokościach h_a i h_b poprowadzonych na te boki dane jest wzorem:
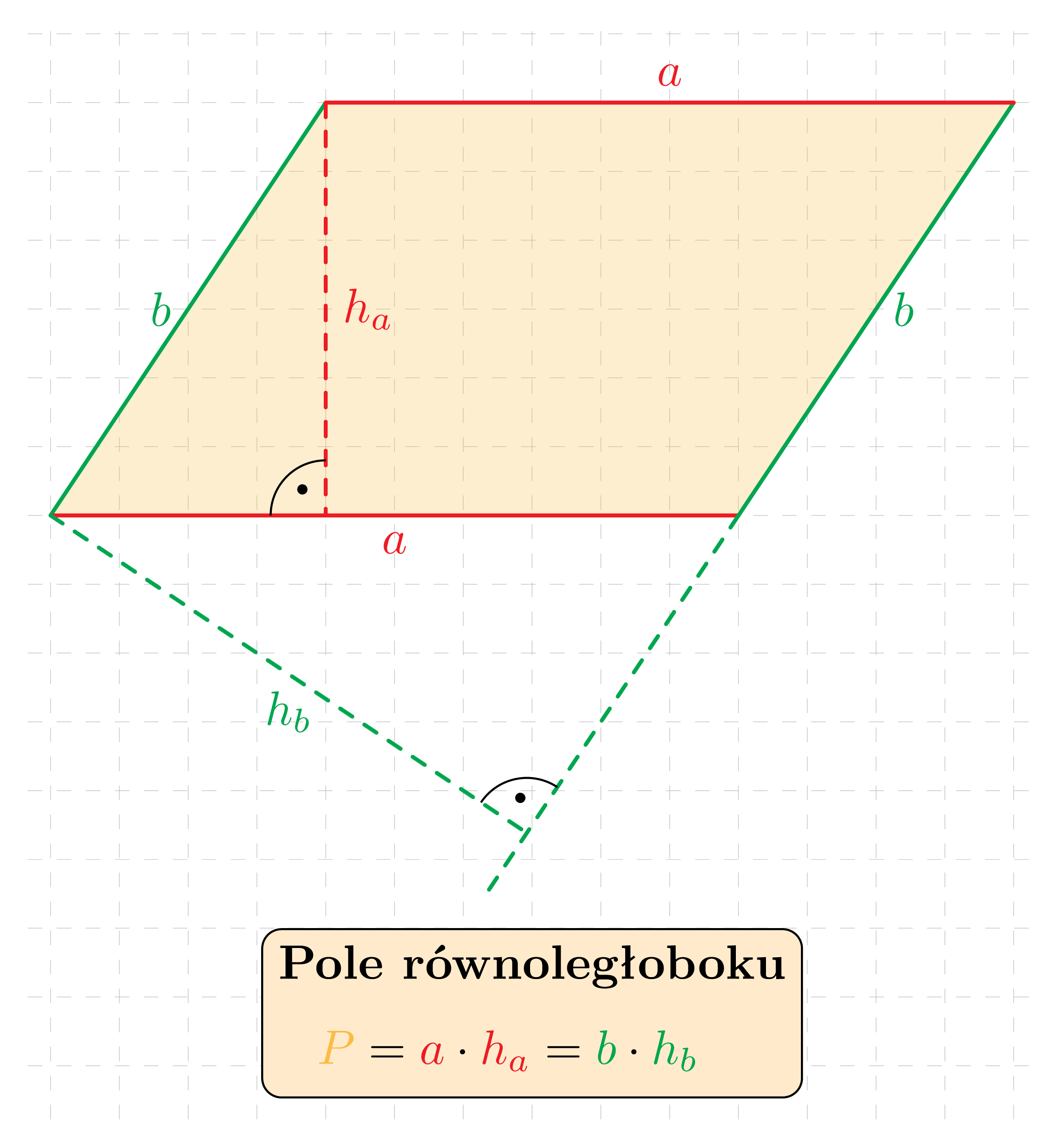
Pole równoległoboku o bokach długości a i b oraz kącie ostrym \alpha wyraża się wzorem:
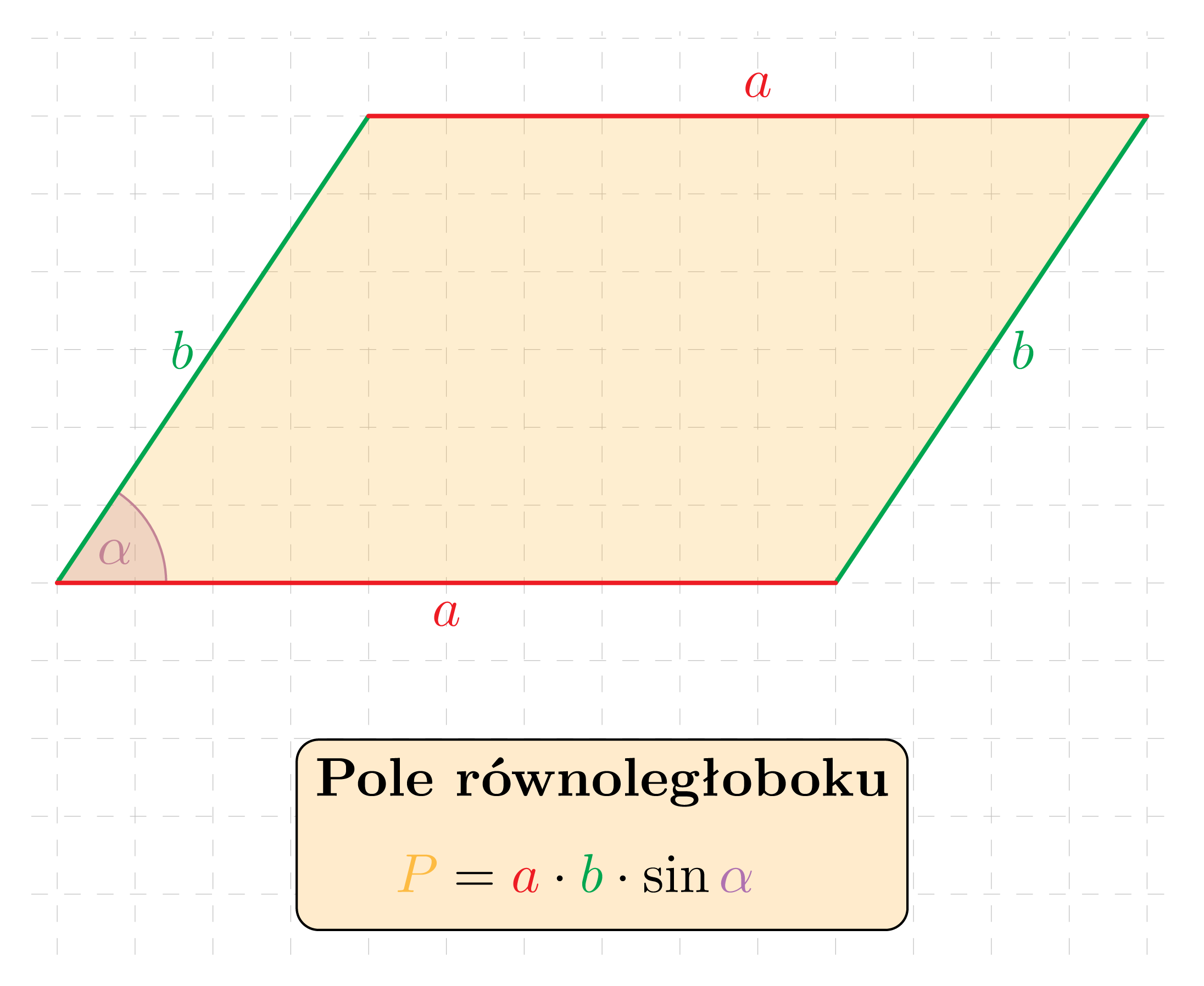
Pole równoległoboku o przekątnych długości d_1 i d_2 oraz kącie ostrym \gamma między nimi wyraża się wzorem:
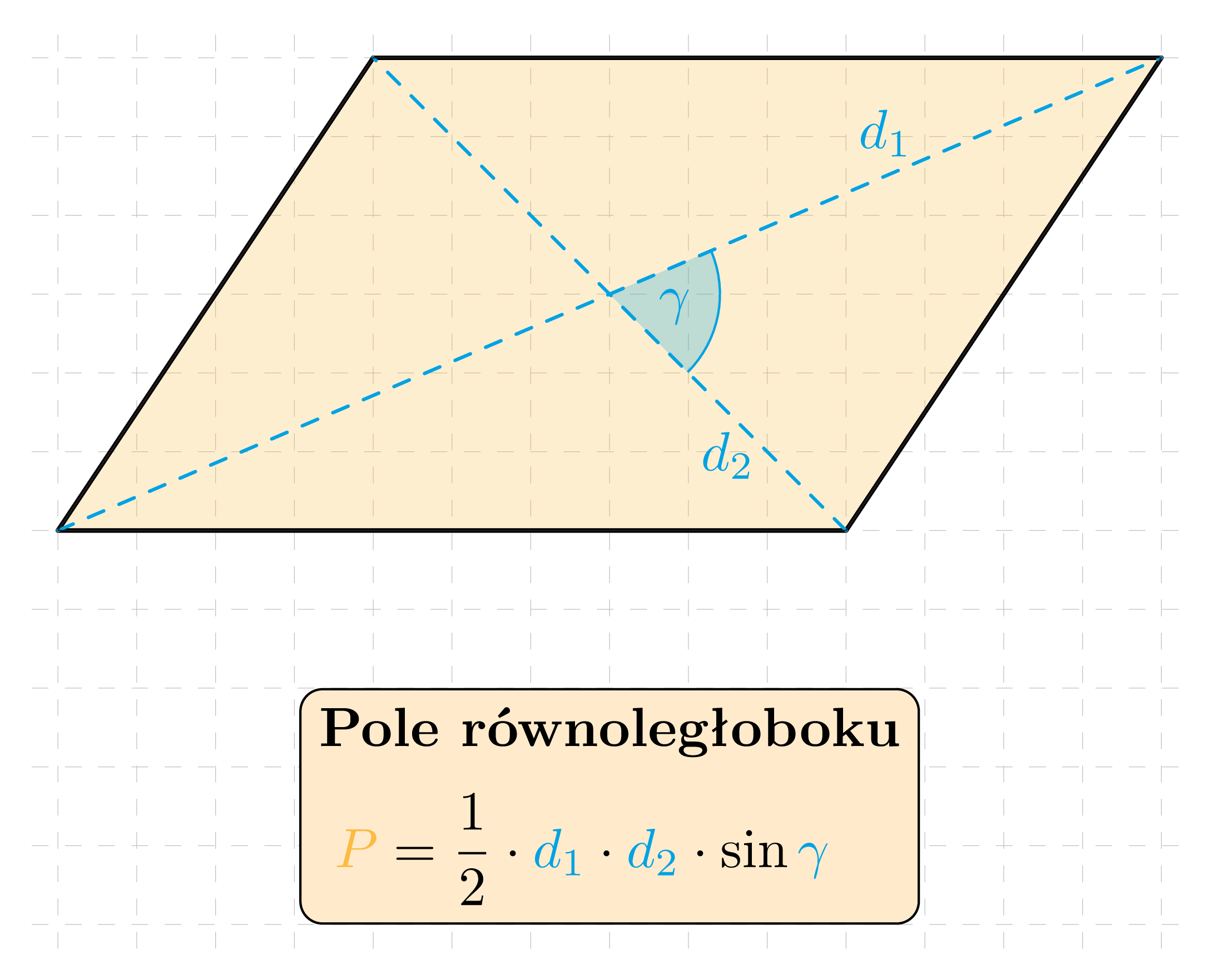

W dowolnym równoległoboku:
kąty znajdujące się w przeciwległych wierzchołkach mają równe miary
suma miar kątów leżących przy tym samym boku wynosi 180^\circ .
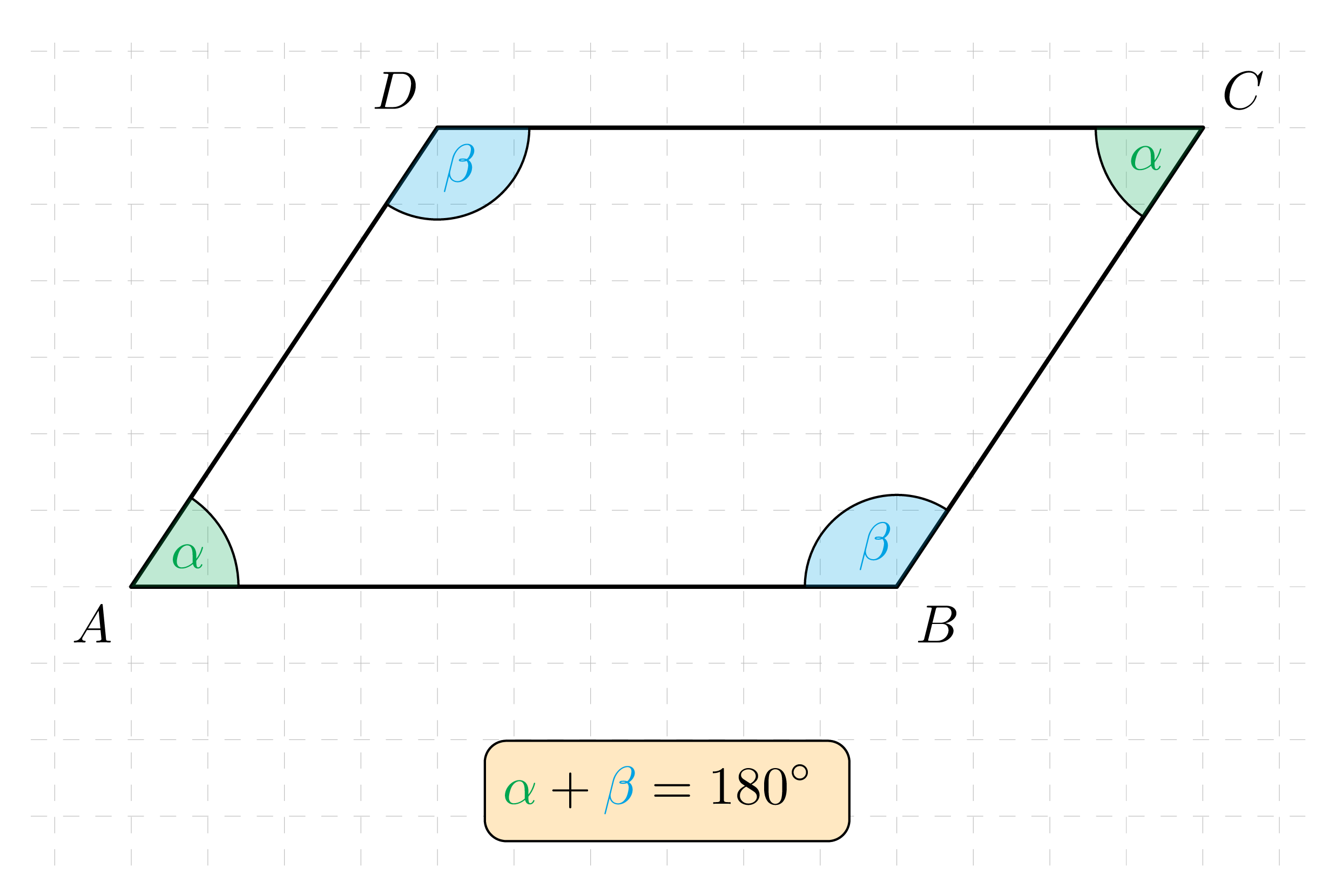
Przekątne równoległoboku przecinają się w połowie

Jeżeli czworokąt spełnia chociaż jeden z poniższych warunków, to czworokąt ten jest równoległobokiem:
wszystkie przeciwległe boki są równej długości,
dwa przeciwległe boki są równoległe i są równej długości,
wszystkie przeciwległe kąty są tej samej miary
suma kątów leżących przy tym samym boku wynosi 180^\circ
przekątne przecinają się w połowie