Stożek to bryła obrotowa otrzymana w wyniku obrotu trójkąta prostokątnego wokół prostej (tzw. oś stożka) zawierającej jedną z jego przyprostokątnych. Podstawą stożka jest koło otrzymane w wyniku obrotu drugiej przyprostokątnej, a wierzchołkiem stożka - wierzchołek trójkąta nienależący do podstawy.

Stożek można również otrzymać obracając trójkąt wokół jego osi symetrii:

Wysokością stożka nazywamy odcinek łączący wierzchołek stożka ze środkiem podstawy (tzw. spodek wysokości stożka).

Tworzącą stożka nazywamy dowolny odcinek łączący wierzchołek stożka z brzegiem podstawy.

Przekrojem osiowym stożka jest trójkąt równoramienny. Powierzchnię stożka można rozłożyć na okrąg (podstawa) oraz wycinek koła (powierzchnia boczna).
Objętość stożka o promieniu podstawy długości r>0 i wysokości H>0 wyraża się wzorem:
Niech dany będzie stożek o promieniu długości r>0 i tworzącej długości H>0. Wówczas:
pole podstawy P_p,
pole powierzchni bocznej P_b,
pole całkowite P_c
tego stożka wyrażają się wzorami:


Przekrojem osiowym stożka jest trójkąt równoramienny o ramieniu długości l oraz podstawie 2r (średnica podstawy stożka).

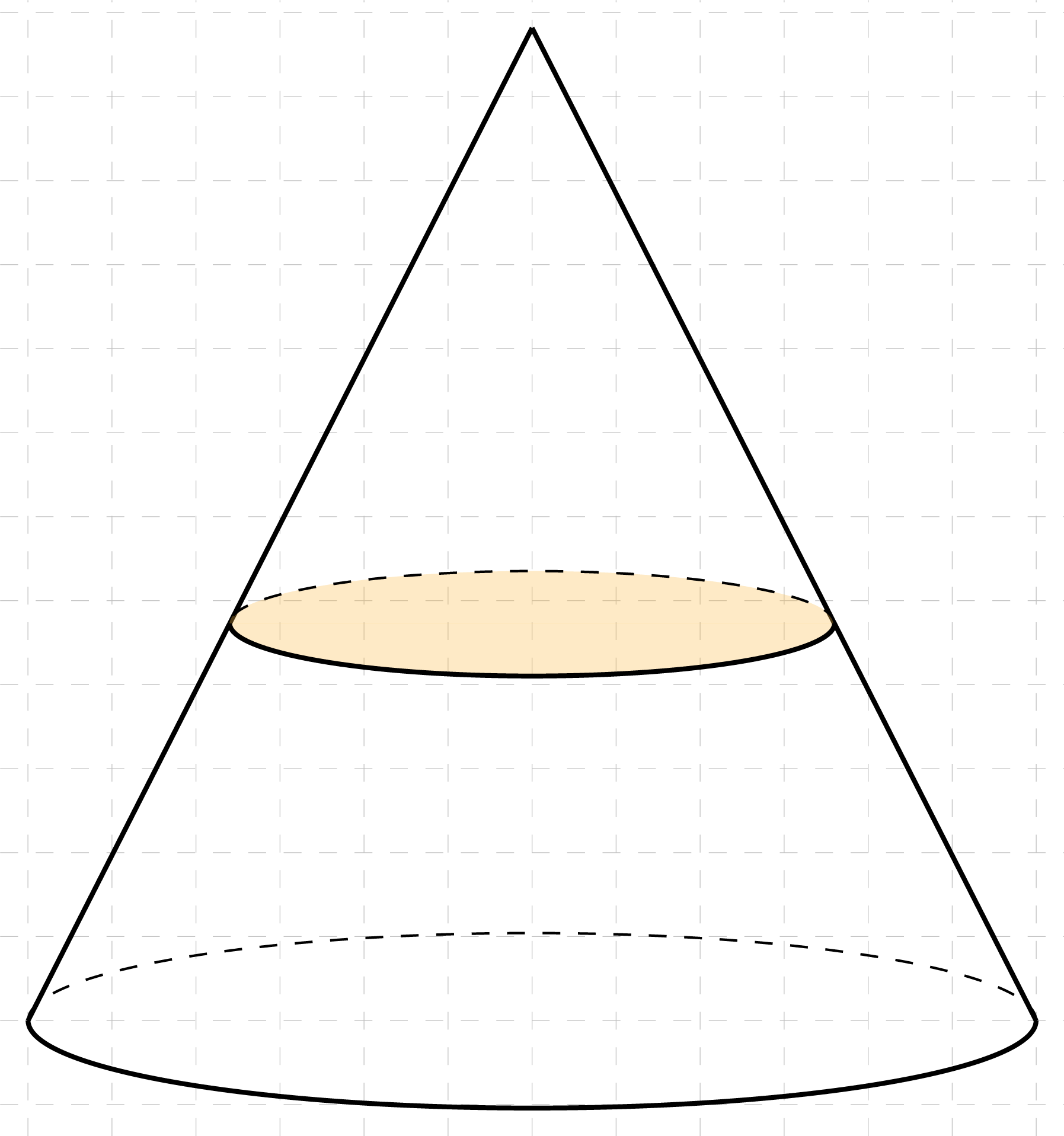
Przekrojem poprzecznym stożka jest koło: