Styczna, sieczna i zewnętrzna okręgu

Styczną do okręgu nazywamy prostą która ma z okręgiem dokładnie jeden punkt wspólny (tzw. punkt styczności prostej i okręgu). Mówimy też że okrąg jest styczny do prostej.

Zauważ, że najkrótszym odcinkiem który łączy środek okręgu ze styczną do tego okręgu jest promień poprowadzony do punktu styczności.

Zachodzą następujące równoważności:

• prosta jest styczną do okręgu wtedy i tylko wtedy, gdy promień tego okręgu poprowadzony do punktu styczności jest prostopadły do tej prostej.

  

• prosta jest styczną do okręgu wtedy i tyko wtedy, gdy odległość środka tego okręgu od tej prostej jest równa promieniowi tego okręgu.
  

  

Sieczną okręgu nazywamy prostą która ma z tym okręgiem dwa punkty wspólne.

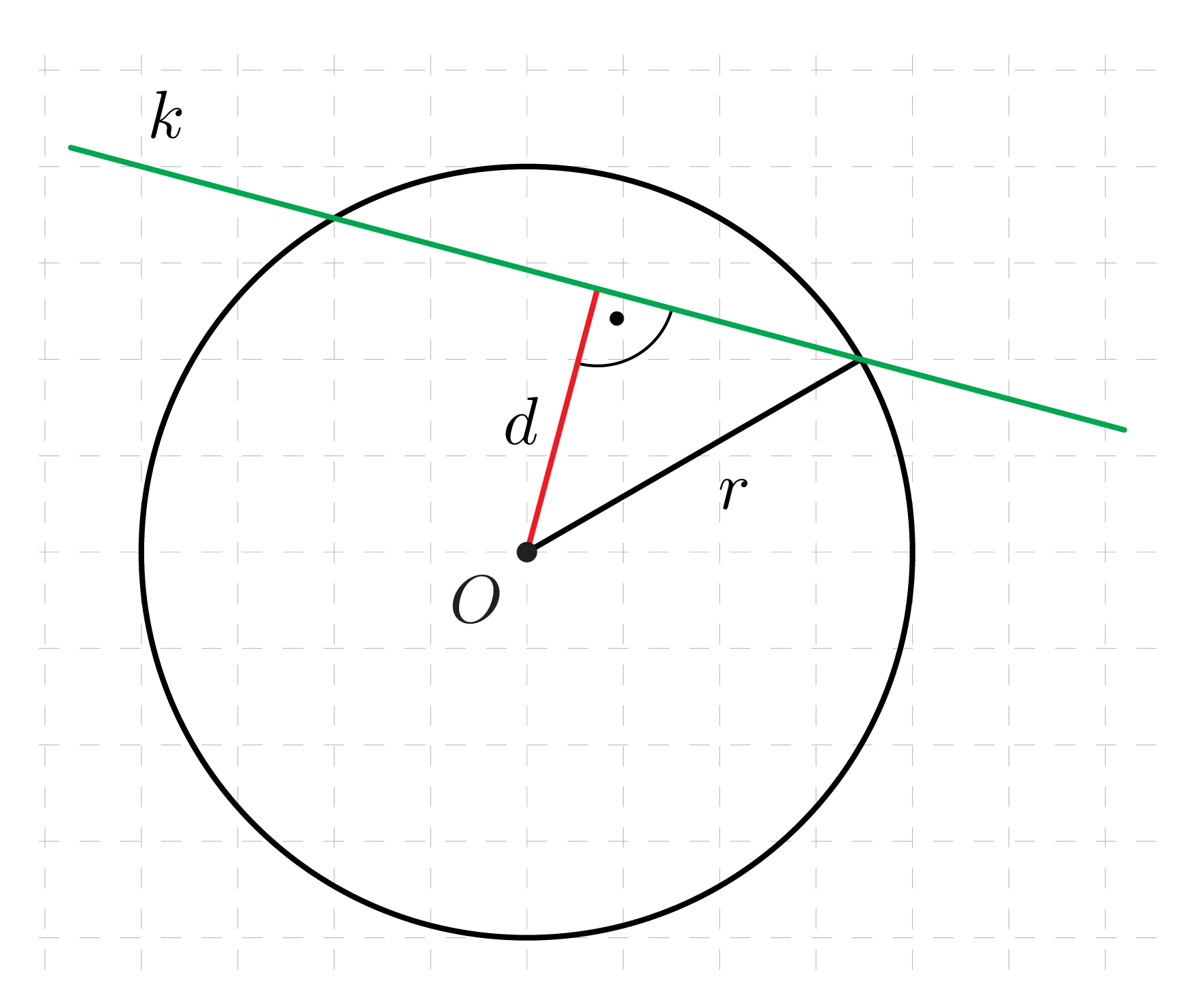
Prosta jest sieczną okręgu wtedy i tyko wtedy, gdy odległość środka tego okręgu od tej prostej jest mniejsza od promienia tego okręgu.

Zewnętrzną okręgu nazywamy dowolną prostą która nie ma z danym okręgiem żadnych punktów wspólnych.

Prosta jest zewnętrzną okręgu wtedy i tyko wtedy, gdy odległość środka tego okręgu od tej prostej jest mniejsza od promienia tego okręgu.

Jeżeli dwie styczne do okręgu w punktach $A$A i $B$B przecinają się w punkcie $P$P, to

Kątem pod jakim widać okrąg nazywamy kąt wypukły utworzony przez dwie styczne do tego okręgu.

Kątem dopisanym do okręgu w punkcie $P$P leżącym na tym okręgu nazywamy kąt wypukły wyznaczony przez styczną do okręgu w punkcie $P$P oraz półprostą zawierającą cięciwę tego okręgu o początku w punkcie punkcie styczności $P$P.

Mówimy też, że kąt ten jest oparty na łuku wyznaczonym przez tę cięciwę.

Kąt dopisany nazywamy również kątem między styczną a cięciwą.

Miara kąta dopisanego jest równa mierze kąta wpisanego opartego na tym samym łuku.

Jeżeli przez punkt $P$P którego odległość od środka danego okręgu jest większa niż promień, poprowadzimy styczną do okręgu w punkt $A$A oraz sieczną przecinającą okrąg w punktach $B$B i $C$C, to zachodzi równość:

Jeżeli dwie proste przecinają okrąg w punktach $A$A i $B$B oraz $C$C i $D$D, a także przecinają się w punkcie $P$P, którego odległość od środka danego okręgu jest większa niż promień tego okręgu, to

Powyższe Twierdzenie jest również prawdziwe gdy sieczne przecinają się wewnątrz okręgu:

Pojęcia stycznej, siecznej i zewnętrznej okręgu dotyczą również koła (jako że okrąg jest jego brzegiem).