Wektory na płaszczyźnie

Wektorem (zaczepionym) nazywamy uporządkowaną parę punktów $[A,B]$[A,B] z których $A=(x_a, y_a)$A=(x_a, y_a) jest początkiem wektora (zwany również punktem zaczepienia), a $B=(x_b, y_b)$B=(x_b, y_b) jest końcem wektora. Wektory oznaczamy małymi literami $\vec{u},\vec{v},\vec{w}, \ldots$\vec{u},\vec{v},\vec{w}, \ldots lub za pomocą punktu początkowego oraz końcowego $\overrightarrow{AB}$\overrightarrow{AB} , a graficznie przedstawiane są w postaci strzałki (odcinka o początku w punkcie $A$A i zakończonego grotem w punkcie $B$B).

Wektorem zerowym $\overrightarrow{0}$\overrightarrow{0} nazywamy wektor którego początek i koniec są tym samym punktem. Jego długość wynosi $0$0 a na płaszczyźnie oznaczamy go za pomocą punktu.

Długością wektora $\overrightarrow{AB}$\overrightarrow{AB} nazywamy długość odcinka $|AB|$|AB| i oznaczamy ją $|\overrightarrow{AB}|$|\overrightarrow{AB}|. Długość wektora o współrzędnych $\vec{u}=[a,b]$\vec{u}=[a,b] dana jest wzorem:

Mówimy, że dwa wektory są równoległe (lub: mają ten sam kierunek), jeżeli leżą na tej samej prostej lub na dwóch prostych równoległych.

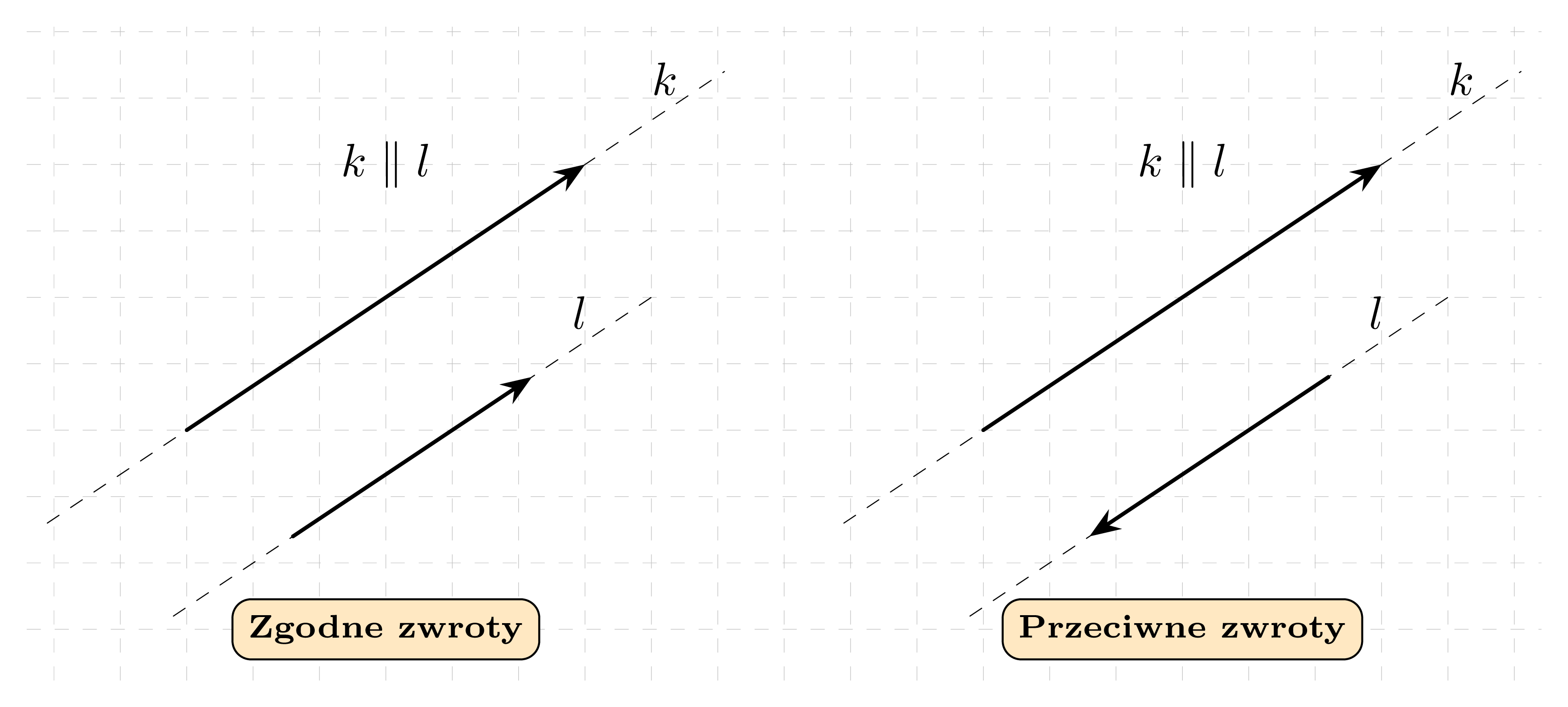
Wektor $\overrightarrow{0}$\overrightarrow{0} nie ma kierunku ani zwrotu.

Mówimy, że dwa wektory są równe, jeżeli mają ten sam zwrot, kierunek i długość.

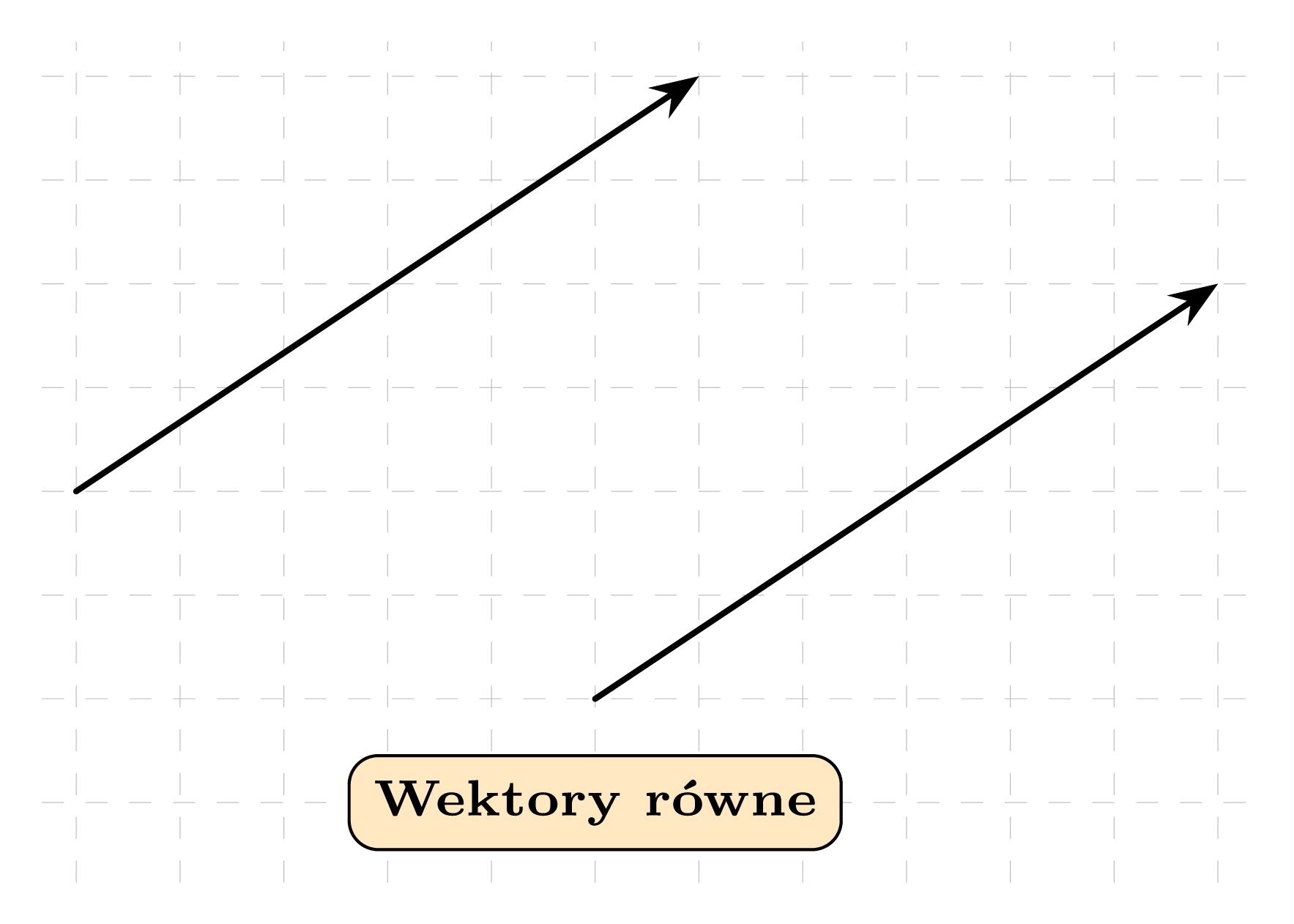
Wektor swobodny to zbiór wszystkich wektorów równych danemu wektorowi.

Sumą wektorów $\overrightarrow{u}$\overrightarrow{u} i $\overrightarrow{v}$\overrightarrow{v} nazywamy wektor $\overrightarrow{u+v}$\overrightarrow{u+v}, którego początek pokrywa się z początkiem wektora $\overrightarrow{u}$\overrightarrow{u}, a koniec odpowiada końcowi wektora $\overrightarrow{v}$\overrightarrow{v} zaczepionego w końcu wektora $\overrightarrow{u}$\overrightarrow{u}.

Jeśli dane są dwa wektory $\vec{u}$\vec{u} i $\vec{v}$\vec{v} zaczepione w tym samym punkcie, to ich suma (wynik dodawania) jest wektorem odpowiadającym przekątnej równoległoboku, którego bokami są te dwa wektory.

Mówimy, że dwa wektory są przeciwne, jeżeli ich suma jest wektorem zerowym. Wektor przeciwny do wektora $\overrightarrow{u}$\overrightarrow{u} oznaczamy $-\overrightarrow{u}$-\overrightarrow{u}.

Odejmowanie wektora $\overrightarrow{v}$\overrightarrow{v} odbywa się poprzez dodanie wektora przeciwnego $-\overrightarrow{v}$-\overrightarrow{v}.

Dwa niezerowe wektory $\overrightarrow{u}$\overrightarrow{u} i $\overrightarrow{v}$\overrightarrow{v} są przeciwne wtedy i tylko wtedy, gdy mają taki sam kierunek i długość, ale przeciwne zwroty.

Niech dane będą wektory $\vec{u}=[a,b]$\vec{u}=[a,b] oraz $\vec{v}=[c,d]$\vec{v}=[c,d]. Wówczas:

• Sumą wektorów $\vec{u}$\vec{u} i $\vec{v}$\vec{v} jest wektor

  $$\vec{u}+\vec{v}=[a+c, b+d]$$

  \vec{u}+\vec{v}=[a+c, b+d](0)

• Różnicą wektorów $\vec{u}$\vec{u} i $\vec{v}$\vec{v} jest wektor:

  $$\vec{u} - \vec{v}=[a-c, b-d]$$

  \vec{u} - \vec{v}=[a-c, b-d](0)

• Iloczynem wektora $\vec{u}$\vec{u} przez liczbę $\alpha\in\mathbb{R}$\alpha\in\mathbb{R} jest wektor:

  $$\alpha\vec{u}=[\alpha a, \alpha b]$$

  \alpha\vec{u}=[\alpha a, \alpha b](0)

Wektor $[0,0]$[0,0] nazywamy wektorem zerowym i oznaczamy go symbolem $\vec{0}$\vec{0}.

Wektorem jednostkowym nazywamy wektor którego długość jest równa $1$1.

Dwa niezerowe wektory $\overrightarrow{u}$\overrightarrow{u} i $\overrightarrow{v}$\overrightarrow{v} są przeciwne wtedy i tylko wtedy, gdy są równoległe, mają przeciwne zwroty oraz taką samą długość.

Iloczynem niezerowego wektora $\overrightarrow{u}$\overrightarrow{u} i liczby $k\neq 0$k\neq 0 nazywamy wektor równoległy do wektora $\overrightarrow{u}$\overrightarrow{u} o długości $|k| \cdot |\overrightarrow{u}|$|k| \cdot |\overrightarrow{u}| oraz zwrocie:

• zgodnym ze zwrotem wektora $\overrightarrow{u}$\overrightarrow{u} jeżeli $k>0$k>0,

• przeciwnym do zwrotu wektora $\overrightarrow{u}$\overrightarrow{u} jeżeli $k<0$k<0.

Iloczyn $\overrightarrow{u}$\overrightarrow{u} i $k$k oznaczamy $k \cdot \overrightarrow{u}$k \cdot \overrightarrow{u}.

Przyjmujemy, że $\overrightarrow{0}\cdot k=\overrightarrow{0}$\overrightarrow{0}\cdot k=\overrightarrow{0} oraz $\overrightarrow{u} \cdot 0=\overrightarrow{0}$\overrightarrow{u} \cdot 0=\overrightarrow{0}.

Dla dowolnych wektorów $\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}$\overrightarrow{u},\overrightarrow{v},\overrightarrow{w} oraz dowolnych $k,l\in\mathbb{R}$k,l\in\mathbb{R} zachodzą następujące własności działań na wektorach:

• przemienność dodawania:

  $$\overrightarrow{u}+\overrightarrow{v}=\overrightarrow{v}+\overrightarrow{u}$$

  \overrightarrow{u}+\overrightarrow{v}=\overrightarrow{v}+\overrightarrow{u}(0)

• łączność dodawania

  $$\overrightarrow{u}+(\overrightarrow{v}+\overrightarrow{w})=(\overrightarrow{u}+\overrightarrow{v})+\overrightarrow{w }$$

  \overrightarrow{u}+(\overrightarrow{v}+\overrightarrow{w})=(\overrightarrow{u}+\overrightarrow{v})+\overrightarrow{w }(0)

• łączność mnożenia skalarnego

  $$k \cdot (l \cdot \overrightarrow{u})=(k \cdot l) \cdot \overrightarrow{u}$$

  k \cdot (l \cdot \overrightarrow{u})=(k \cdot l) \cdot \overrightarrow{u}(0)

• rozdzielność mnożenia względem dodawania skalarów

  $$(k+l) \cdot \overrightarrow{u}=k \cdot \overrightarrow{u}+l \cdot \overrightarrow{u}$$

  (k+l) \cdot \overrightarrow{u}=k \cdot \overrightarrow{u}+l \cdot \overrightarrow{u}(0)

• rozdzielnością mnożenia skalarnego względem dodawania wektorów

  $$k \cdot ( \overrightarrow{u}+ \overrightarrow{v})=k \cdot \overrightarrow{u}+k \cdot \overrightarrow{u}$$

  k \cdot ( \overrightarrow{u}+ \overrightarrow{v})=k \cdot \overrightarrow{u}+k \cdot \overrightarrow{u}(0)

  
  

  
  

Powinowactwem prostokątnym o osi $s$s i skali $k\neq0$k\neq0 nazywamy przekształcenie geometryczne w którym obrazem dowolnego punktu $A$A jest punkt $A'$A' taki że

gdzie $P$P jest punktem przecięcia prostej $AA'$AA' oraz prostej $s$s.

W powinowactwie prostokątnym obrazem dowolnej prostej jest prosta.