Wektory w układzie współrzędnych

Niech w układzie współrzędnych dane będą punkty $A=(x_A,y_A)$A=(x_A,y_A) i $B=(x_B,y_B)$B=(x_B,y_B). Wektorem $\overrightarrow{AB}$\overrightarrow{AB} nazywamy uporządkowaną parę liczb $[x_B-x_A,y_B-y_A]$[x_B-x_A,y_B-y_A], gdzie liczby $x_B-x_A$x_B-x_A i $y_B-y_A$y_B-y_A nazywamy współrzędnymi tego wektora.

Wektorem zerowym nazywamy wektor (w układzie współrzędnych oznaczamy jako punkt) którego obie współrzędne są równe $0$0, tj. $\overrightarrow{0}=[0,0]$\overrightarrow{0}=[0,0].

Mówimy, że dwa wektory $\overrightarrow{u}=[u_x,u_y]$\overrightarrow{u}=[u_x,u_y] i $\overrightarrow{v}=[v_x, v_y]$\overrightarrow{v}=[v_x, v_y] są równe, co zapisujemy $\overrightarrow{u}=\overrightarrow{v}$\overrightarrow{u}=\overrightarrow{v}, jeżeli $u_x=v_x$u_x=v_x oraz $u_y=v_y$u_y=v_y.

Wektorem swobodnym nazywamy zbiór wszystkich wektorów równych danemu wektorowi (wektor nie ma określonego początku ani końca, a jedynie współrzędne).

Długością wektora $\overrightarrow{u}=[u_x,u_y]$\overrightarrow{u}=[u_x,u_y] nazywamy liczbę daną wzorem:

Długość wektora $\overrightarrow{AB}$\overrightarrow{AB} gdzie $A=(x_A,y_A)$A=(x_A,y_A) i $B=(x_B,y_B)$B=(x_B,y_B) dana jest wzorem:

Wektorem jednostkowym (wersorem) nazywamy wektor o długości $1$1.

Dowolny wektor możemy zamienić na wektor jednostkowy dzieląc jego współrzędne przez długość.

Sumą wektorów $\overrightarrow{u}=[u_x,u_y]$\overrightarrow{u}=[u_x,u_y] i $\overrightarrow{v}=[v_x,v_y]$\overrightarrow{v}=[v_x,v_y] nazywamy wektor $\overrightarrow{u}+\overrightarrow{v}=[u_x+v_x,u_y+v_y]$\overrightarrow{u}+\overrightarrow{v}=[u_x+v_x,u_y+v_y].

Wektory $\overrightarrow{u}=[u_x,u_y]$\overrightarrow{u}=[u_x,u_y] i $\overrightarrow{v}=[v_x,v_y]$\overrightarrow{v}=[v_x,v_y] nazywamy wektorami przeciwnymi, jeżeli ich suma jest wektorem zerowym, czyli zachodzi $u_x+v_x=0$u_x+v_x=0 oraz $u_y+v_y=0$u_y+v_y=0. Wektor przeciwny do wektora $\overrightarrow{u}$\overrightarrow{u} oznaczamy $-\overrightarrow{u}$-\overrightarrow{u}.

Zauważ, że musi zachodzić: $-\overrightarrow{u}=[-u_x, -u_y]$-\overrightarrow{u}=[-u_x, -u_y].

Różnicą wektorów $\overrightarrow{u}=[u_x,u_y]$\overrightarrow{u}=[u_x,u_y] i $\overrightarrow{v}=[v_x,v_y]$\overrightarrow{v}=[v_x,v_y] nazywamy wektor $\overrightarrow{u}-\overrightarrow{v}=[u_x-v_x,u_y-v_y]$\overrightarrow{u}-\overrightarrow{v}=[u_x-v_x,u_y-v_y].

Iloczynem wektora $\overrightarrow{u}=[u_x,u_y]$\overrightarrow{u}=[u_x,u_y] przez liczbę $k\in\mathbb{R}$k\in\mathbb{R} nazywamy wektor $k \cdot \overrightarrow{u}=[k \cdot u_x,k \cdot u_y]$k \cdot \overrightarrow{u}=[k \cdot u_x,k \cdot u_y].

Mówimy, że wektory $\overrightarrow{u}$\overrightarrow{u} i $\overrightarrow{v}$\overrightarrow{v} są równoległe (mają ten sam kierunek), jeżeli istnieje $k\in\mathbb{R}$k\in\mathbb{R} takie że $\overrightarrow{u}=k \cdot \overrightarrow{v}$\overrightarrow{u}=k \cdot \overrightarrow{v} . Jeżeli $k>0$k>0 to mówimy, że wektory mają ten sam zwrot, a jeżeli $k<0$k<0 to mówimy, że wektory te mają przeciwne zwroty. Dodatkowo, przyjmujemy że wektor zerowy $\overrightarrow{0}$\overrightarrow{0} jest równoległy do każdego wektora.

Niezerowe wektory $\overrightarrow{u}$\overrightarrow{u} i $\overrightarrow{v}$\overrightarrow{v} są równe wtedy i tylko wtedy, gdy mają tę samą długość, są równoległe oraz mają ten sam zwrot.

Niezerowe wektory $\overrightarrow{u}$\overrightarrow{u} i $\overrightarrow{v}$\overrightarrow{v} są przeciwne wtedy i tylko wtedy, gdy mają tę samą długość, są równoległe oraz mają przeciwne zwroty.

Dla dowolnych wektorów $\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}$\overrightarrow{u},\overrightarrow{v},\overrightarrow{w} w układzie współrzędnych oraz dowolnych $k,l\in\mathbb{R}$k,l\in\mathbb{R} zachodzą następujące własności działań na wektorach:

• przemienność dodawania:

  $$\overrightarrow{u}+\overrightarrow{v}=\overrightarrow{v}+\overrightarrow{u}$$

  \overrightarrow{u}+\overrightarrow{v}=\overrightarrow{v}+\overrightarrow{u}(0)

• łączność dodawania

  $$\overrightarrow{u}+(\overrightarrow{v}+\overrightarrow{w})=(\overrightarrow{u}+\overrightarrow{v})+\overrightarrow{w }$$

  \overrightarrow{u}+(\overrightarrow{v}+\overrightarrow{w})=(\overrightarrow{u}+\overrightarrow{v})+\overrightarrow{w }(0)

• łączność mnożenia skalarnego

  $$k \cdot (l \cdot \overrightarrow{u})=(k \cdot l) \cdot \overrightarrow{u}$$

  k \cdot (l \cdot \overrightarrow{u})=(k \cdot l) \cdot \overrightarrow{u}(0)

• rozdzielność mnożenia względem dodawania skalarów

  $$(k+l) \cdot \overrightarrow{u}=k \cdot \overrightarrow{u}+l \cdot \overrightarrow{u}$$

  (k+l) \cdot \overrightarrow{u}=k \cdot \overrightarrow{u}+l \cdot \overrightarrow{u}(0)

• rozdzielnością mnożenia skalarnego względem dodawania wektorów

  $$k \cdot ( \overrightarrow{u}+ \overrightarrow{v})=k \cdot \overrightarrow{u}+k \cdot \overrightarrow{u}$$

  k \cdot ( \overrightarrow{u}+ \overrightarrow{v})=k \cdot \overrightarrow{u}+k \cdot \overrightarrow{u}(0)

  
  

Przesunięcie równoległe (translacja) o wektor $\overrightarrow{u}=[u_x,y_y]$\overrightarrow{u}=[u_x,y_y] to przekształcenie geometryczne $T_{\overrightarrow{u}}$T_{\overrightarrow{u}} które każdemu punktowi $A=\left(x,y\right)$A=\left(x,y\right) przyporządkowuje punkt $A'$A', dla którego $\overrightarrow{AA'}=\overrightarrow{u}$\overrightarrow{AA'}=\overrightarrow{u}, tj.

W układzie współrzędnych obrazem punktu $A=\left(x,y\right)$A=\left(x,y\right) w przesunięciu o wektor $\overrightarrow{u}=[u_x,y_y]$\overrightarrow{u}=[u_x,y_y] jest punkt $A'=\left(x+u_x,y+u_y\right)$A'=\left(x+u_x,y+u_y\right).

Przesunięcie o wektor nie zmienia ani rozmiaru, ani kształtu figury.

W kartezjańskim układzie współrzędnych obrazem punktu $A=(x,y)$A=(x,y) w przesunięciu równoległym o wektor $\overrightarrow{u}=[p,q]$\overrightarrow{u}=[p,q] jest punkt $A'=[x+p,y+q]$A'=[x+p,y+q].

Jeżeli przesuwamy o wektor $\overrightarrow{u}=[p,0]$\overrightarrow{u}=[p,0] to mówimy o przesunięciu równoległym wzdłuż osi $OX$OX, a jeżeli $\overrightarrow{u}=[0,q]$\overrightarrow{u}=[0,q] to mówimy o przesunięciu równoległym wzdłuż osi $OY$OY.

Obrazem punktu $A=(x,y)$A=(x,y) w powinowactwie prostokątnym o osi $OX$OX i skali $k\neq 0$k\neq 0 jest punkt $A'=\left(x,k \cdot y\right)$A'=\left(x,k \cdot y\right).

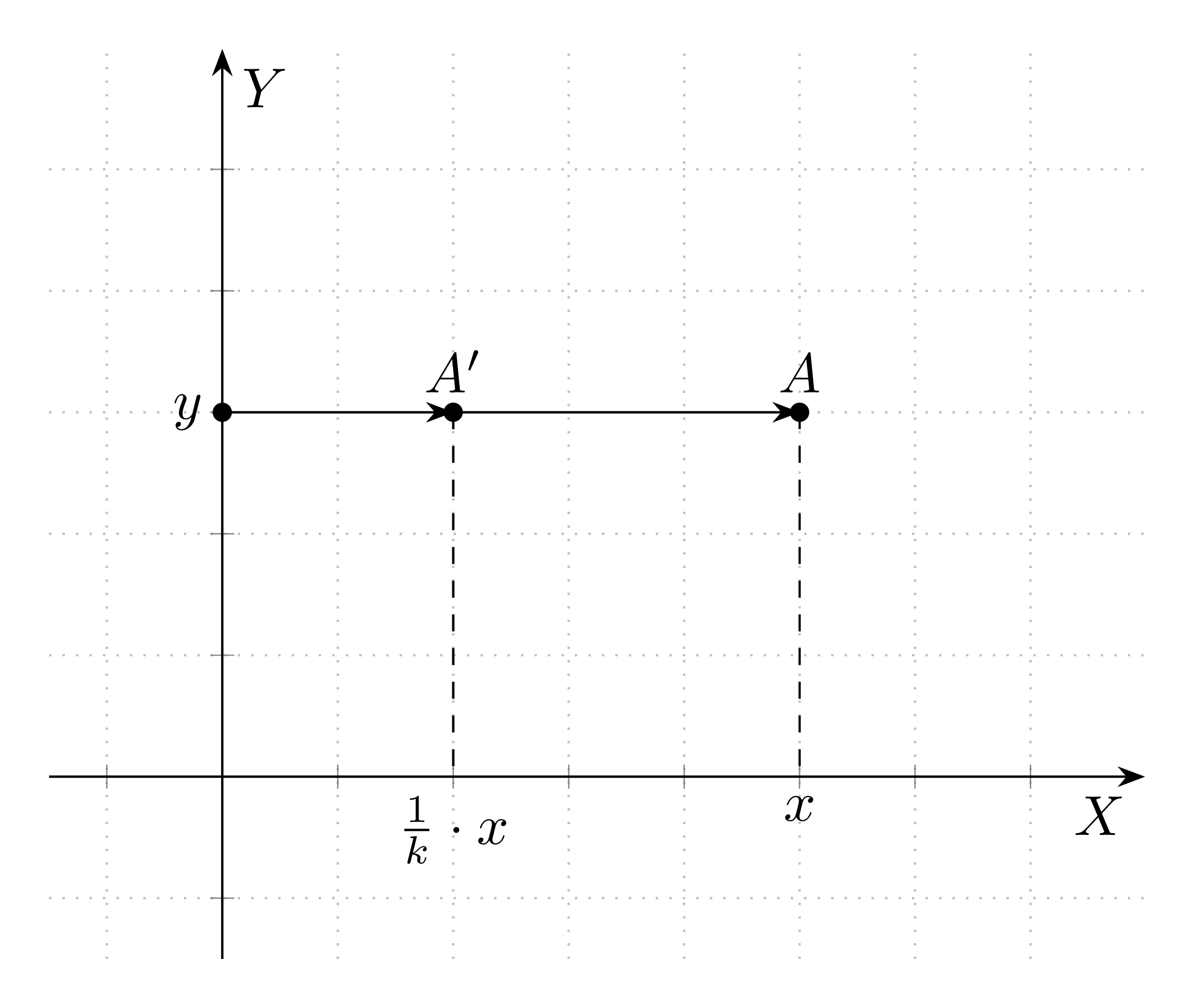
Obrazem punktu $A=(x,y)$A=(x,y) w powinowactwie prostokątnym o osi $OY$OY i skali $\displaystyle \frac{1}{k},k\neq 0$\displaystyle \frac{1}{k},k\neq 0 jest punkt $\displaystyle A'=\left(\frac{1}{k} \cdot x,y\right)$\displaystyle A'=\left(\frac{1}{k} \cdot x,y\right).

Kątem utworzonym przez dwa niezerowe wektory $\overrightarrow{u}$\overrightarrow{u} i $\overrightarrow{v}$\overrightarrow{v} nazywamy kąt wypukły $AOB$AOB, gdzie $\overrightarrow{OA}=\overrightarrow{u}$\overrightarrow{OA}=\overrightarrow{u} i $\overrightarrow{OB}=\overrightarrow{v}$\overrightarrow{OB}=\overrightarrow{v} . Oznaczenie: $\measuredangle(\overrightarrow{u},\overrightarrow{v})$\measuredangle(\overrightarrow{u},\overrightarrow{v}).

Kąt $\alpha$\alpha utworzony przez dwa niezerowe wektory $\overrightarrow{u}=\left[u_1,u_2\right]$\overrightarrow{u}=\left[u_1,u_2\right] i $\overrightarrow{v}=\left[v_1,v_2\right]$\overrightarrow{v}=\left[v_1,v_2\right] spełnia zależności:

Mówimy, że wektory $\overrightarrow{u}$\overrightarrow{u} i $\overrightarrow{v}$\overrightarrow{v} są prostopadłe gdy kąt utworzony przez te wektory jest kątem prostym.

Dla wektorów $\overrightarrow{u}=\left[u_1,u_2\right]$\overrightarrow{u}=\left[u_1,u_2\right] i $\overrightarrow{v}=\left[v_1,v_2\right]$\overrightarrow{v}=\left[v_1,v_2\right] zachodzą następujące równoważności:

• $\displaystyle \overrightarrow{u}\perp \overrightarrow{v}\iff u_1v_1+u_2v_2=0$\displaystyle \overrightarrow{u}\perp \overrightarrow{v}\iff u_1v_1+u_2v_2=0

• $\displaystyle \overrightarrow{u}\parallel\overrightarrow{v}\iff u_1v_2-u_2v_1=0$\displaystyle \overrightarrow{u}\parallel\overrightarrow{v}\iff u_1v_2-u_2v_1=0

Równanie prostej przechodzącej przez punkt $P=\left(x_0,y_0\right)$P=\left(x_0,y_0\right) oraz prostopadłej do wektora $\overrightarrow{u}=\left[p,q\right]$\overrightarrow{u}=\left[p,q\right] dane jest wzorem: