Wykresy funkcji trygonometrycznych
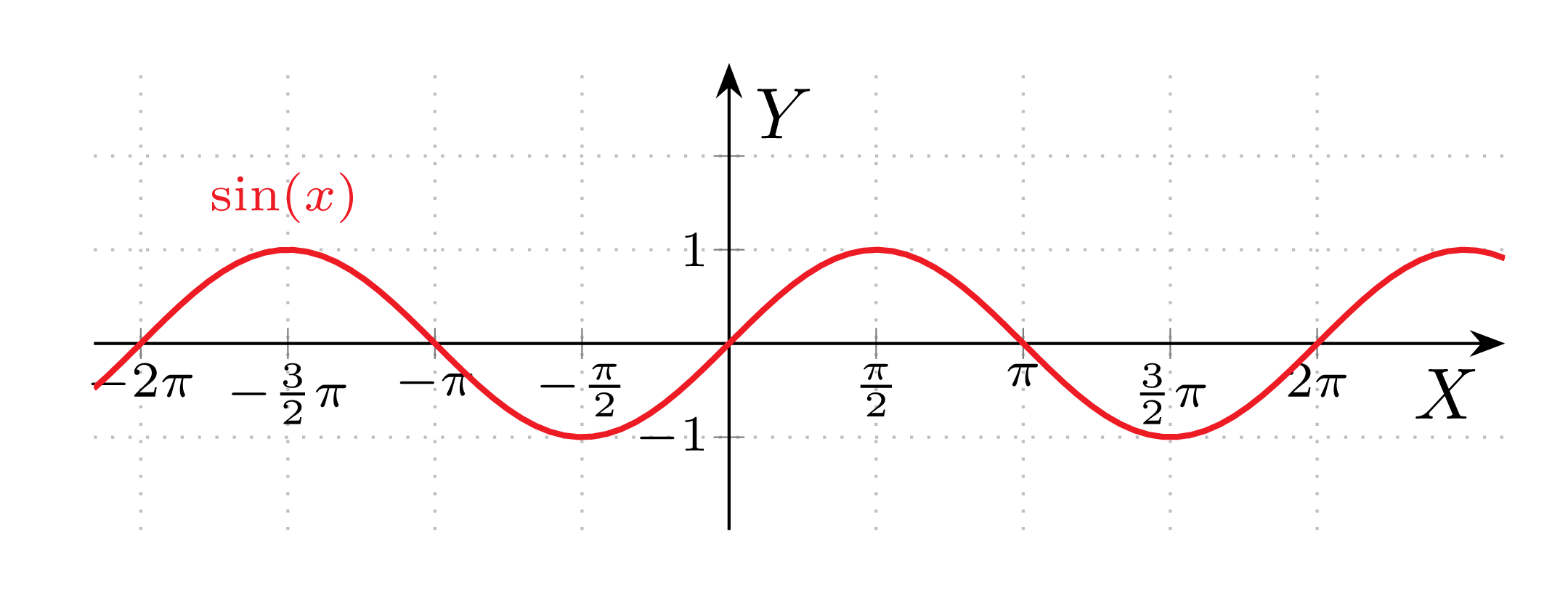
Sinus
Niech dana będzie funkcja f(x)=\sin(x). Wówczas:
Dziedzina D=\mathbb{R}
Zbiór wartości \text{ZW}=\left[-1,1\right]
Miejsca zerowe \left\{x:x= \frac{\pi }{2}+ k\pi, k\in\mathbb{Z}\right\}
Monotoniczność:
rosnąca w przedziałach \displaystyle \left[- \frac{\pi}{2}+2k\pi, \frac{\pi}{2}+2k\pi \right], k\in\mathbb{Z}
malejąca w przedziałach \displaystyle \left[\frac{\pi}{2}+2k\pi, \frac{3\pi}{2}+2k\pi \right], k\in\mathbb{Z}
Funkcja jest nieparzysta
Funkcja jest okresowa z okresem podstawowym T=2\pi
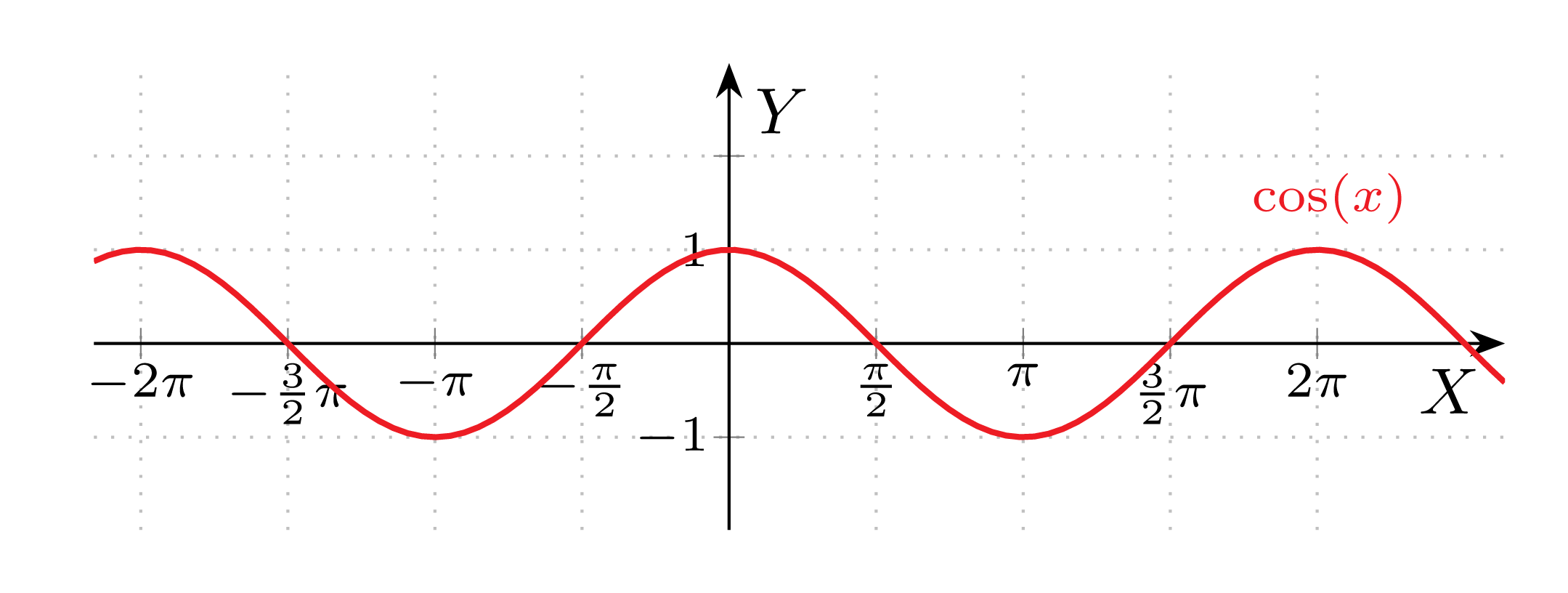
Cosinus
Niech dana będzie funkcja f(x)=\cos(x). Wówczas:
Dziedzina D=\mathbb{R}
Zbiór wartości \text{ZW}=\left[-1,1\right]
Miejsca zerowe \displaystyle \left\{x:x= \frac{\pi}{2}+ k\pi, k\in\mathbb{Z}\right\}
Monotoniczność:
rosnąca w przedziałach \displaystyle \left[2k\pi, \pi +2k\pi \right], k\in\mathbb{Z}
malejąca w przedziałach \displaystyle \left[\pi +2k\pi,2\pi +2k\pi \right], k\in\mathbb{Z}
Funkcja jest parzysta
Funkcja jest okresowa z okresem podstawowym T=2\pi
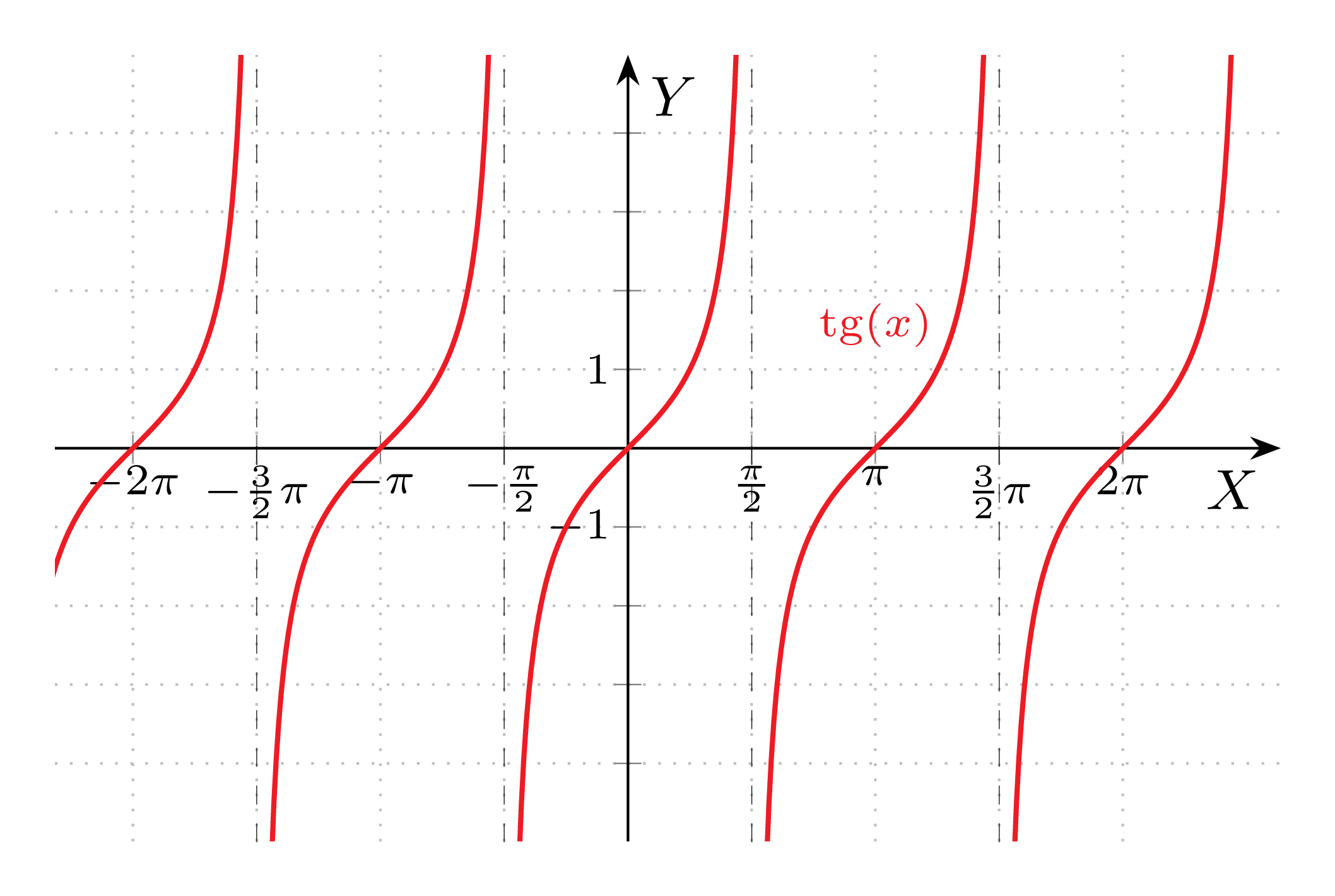
Tangens
Niech dana będzie funkcja f(x)=\tg(x). Wówczas:
Dziedzina D=\mathbb{R}\setminus\left\{ \frac{\pi}{2}+k\pi, k\in\mathbb{Z} \right\}
Zbiór wartości \text{ZW}=\mathbb{R}
Miejsca zerowe \displaystyle \left\{x:x= k\pi, k\in\mathbb{Z}\right\}
Rosnąca w przedziałach \displaystyle \left(- \frac{\pi}{2}+k\pi , \frac{\pi}{2} +k\pi \right), k\in\mathbb{Z}
Funkcja jest nieparzysta
Funkcja jest okresowa z okresem podstawowym T=\pi
Cotangens
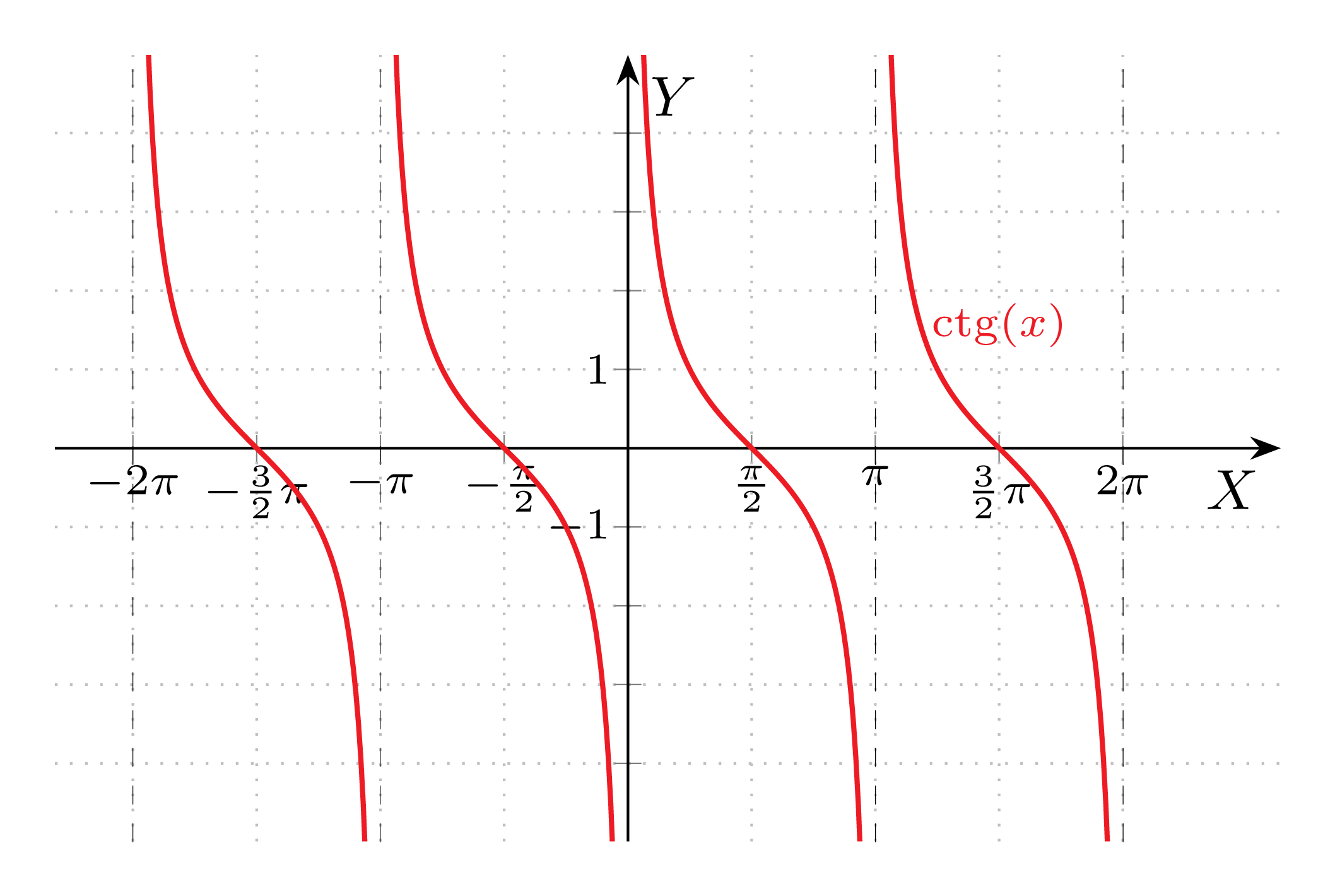
Dziedzina D=\mathbb{R}\setminus\left\{ k\pi, k\in\mathbb{Z} \right\}
Zbiór wartości \text{ZW}=\mathbb{R}
Miejsca zerowe \displaystyle \left\{x:x= \frac{\pi}{2}+ k\pi, k\in\mathbb{Z}\right\}
Malejąca w przedziałach \displaystyle \left(-k\pi , -k\pi + \pi \right), k\in\mathbb{Z}
Funkcja jest nieparzysta
Funkcja jest okresowa z okresem podstawowym T=\pi