Definicja
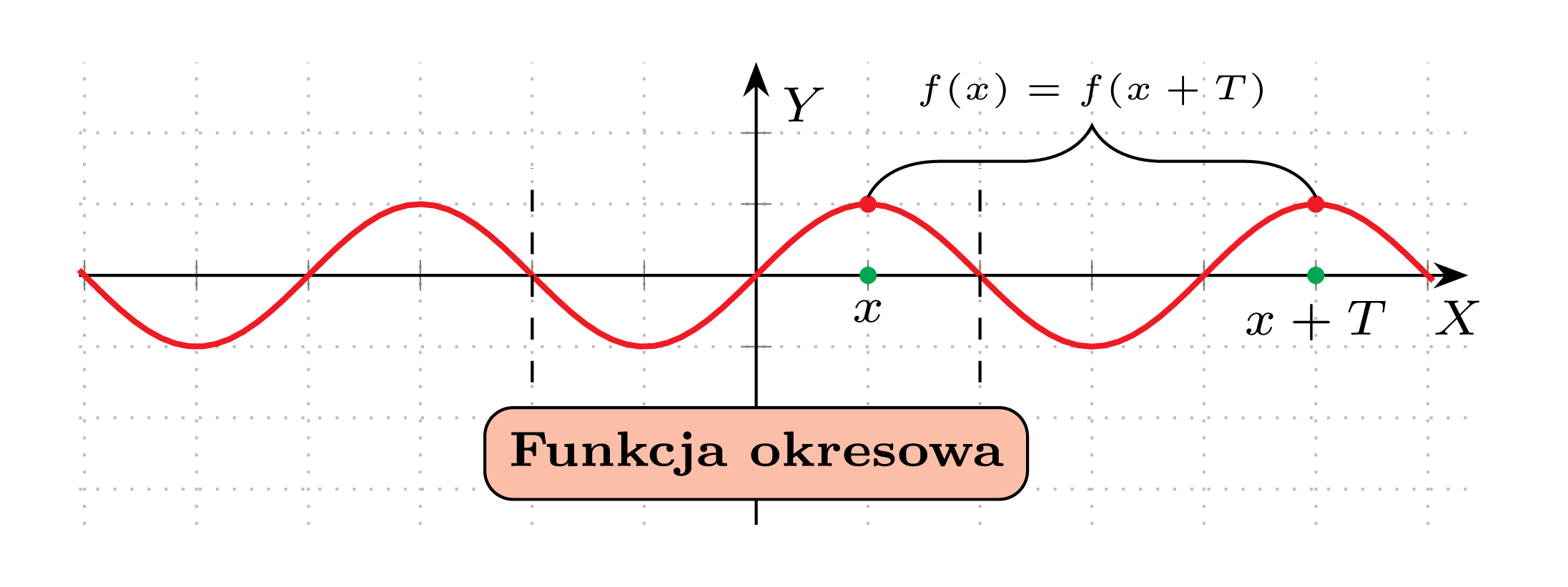
Funkcja okresowa
Mówimy, że funkcja f:D\subset\mathbb{R}\rightarrow\mathbb{R} jest okresowa, jeżeli istnieje liczba T\neq0, taka że dowolnego x\in D, liczba x+T\in D oraz zachodzi równość
Liczbę T nazywamy okresem funkcji f a o samej funkcji f możemy również powiedzieć że jest funkcją T-okresową. Jeżeli istnieje najmniejszy okres dodatni funkcji f, to nazywamy go okresem podstawowym (lub zasadniczym) i oznaczamy go T_0.
Dowiedz się więcej!
Więcej informacji o pojęciu Funkcja okresowa znajdziesz w: