Okrąg w układzie współrzędnych

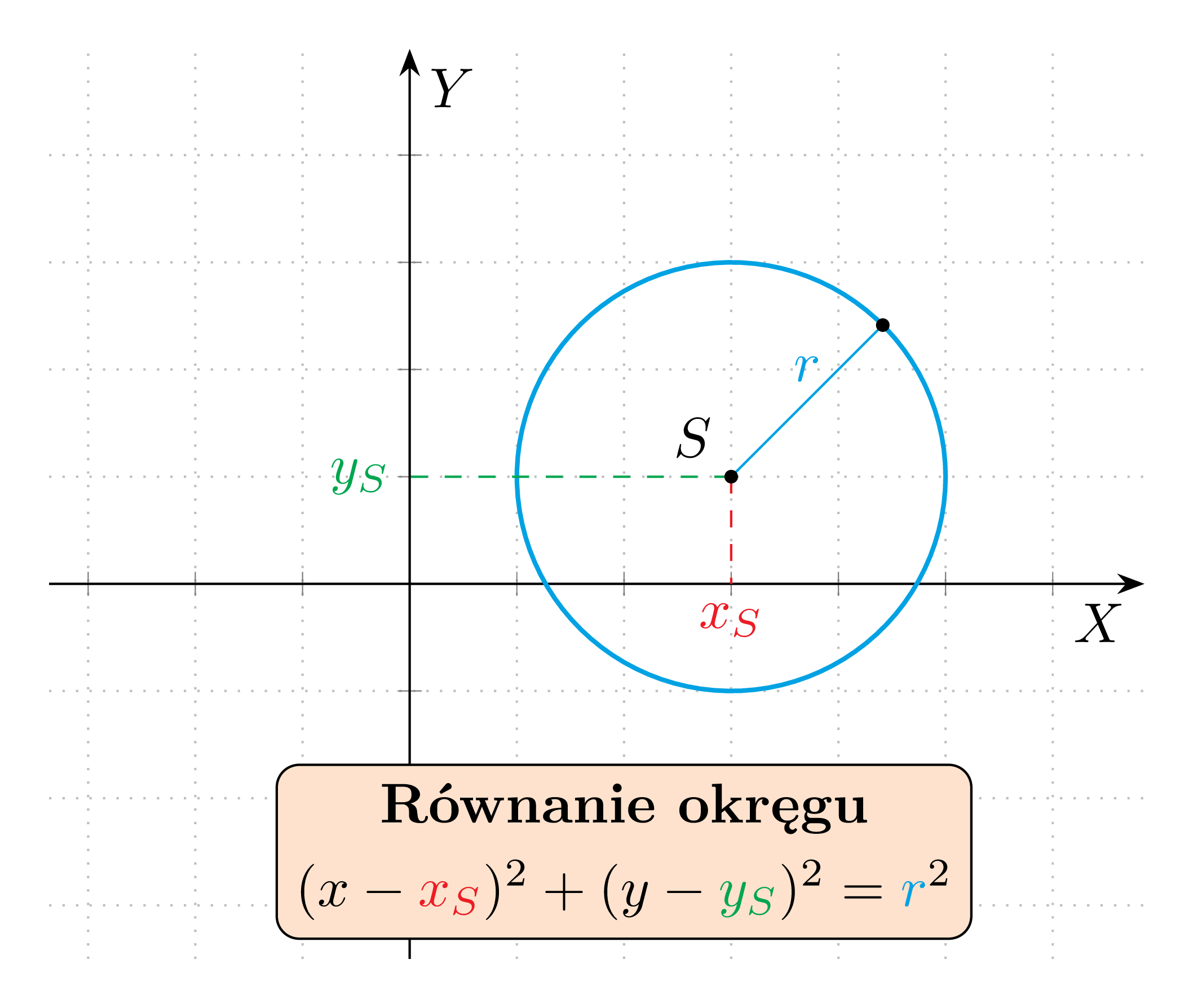
Okrąg o środku w punkcie $(x_S,y_S)$ (x_S,y_S) i promieniu $r>0$ r>0 jest zbiorem wszystkich punktów płaszczyzny $(x,y)\in\mathbb{R^2}$ (x,y)\in\mathbb{R^2} spełniających równanie:

(x-x_S)^2+(y-y_S)^2=r^2

(0)

Równanie to nazywamy równaniem okręgu w postaci kanonicznej.

Dowiedz się więcej!

Więcej informacji o pojęciu Okrąg w układzie współrzędnych znajdziesz w:

Okrąg i koło w układzie współrzędnych