Definicja
Przedział domknięty
Historia występowania na egzaminach
Sprawdź historię występowania zadań tego typu na dotychczasowych egzaminach.
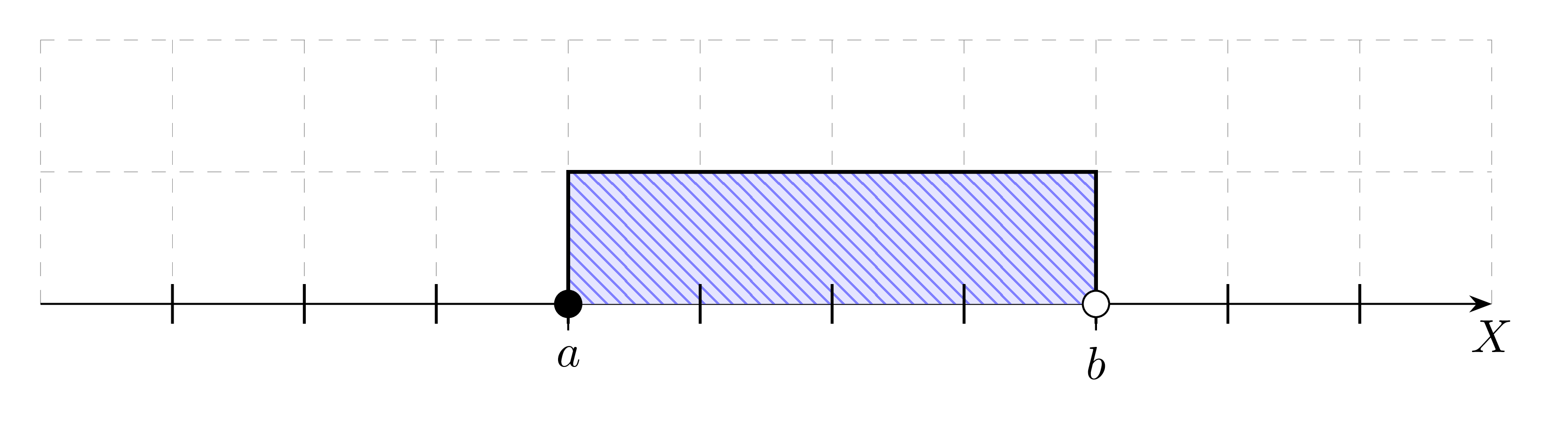
Przedziałem domkniętym (obustronnie domkniętym) od a do b (a,b\in\mathbb{R},a<b) nazywamy zbiór liczb rzeczywistych większych bądź równych a oraz jednocześnie mniejszych bądź równych b. Zapisujemy:

Jeśli do przedziału należy tylko jego lewy koniec, to mówimy o przedziale lewostronnie domkniętym, a jeśli do przedziału należy tylko jego prawy koniec to mówimy o przedziale prawostronnie domkniętym. Zapisujemy odpowiednio:

Dowiedz się więcej!
Więcej informacji o pojęciu Przedział domknięty znajdziesz w: