Znając współrzędne punktów A i B możemy obliczyć odległość między nimi lub inaczej, długość odcinka AB. Wzór na długość odcinka wynika z Twierdzenia Pitagorasa.

Twierdzenie 1

Wzór na długość odcinka w układzie współrzędnych (odległość między punktami w układzie współrzędnych)

Odległość między punktami A=(x_A,y_A) i B=(x_B, y_B) (tj. długość odcinka AB) w układzie współrzędnych wyraża się wzorem:

(0)|AB|=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}

W szczególności:

jeżeli y_A=y_B (odcinek AB jest równoległy do osi OX), to
(0)|AB|=|x_B-x_A|
jeżeli x_A=x_B (odcinek AB jest równoległy do osi OY), to
(0)|AB|=|y_B-y_A|

Twierdzenie 2

O odległości między prostymi równoległymi

Odległość między prostymi k i l danych równaniami:

(0)\begin{aligned} k:Ax+By+C=0\\ l:Ax+By+C'=0 \end{aligned}

gdzie A^2+B^2\neq 0 wyraża się wzorem:

(0)\displaystyle d(k,l)= \frac{|C'-C|}{\sqrt{A^2+B^2}}

Twierdzenie 3

Wzór na środek odcinka w układzie współrzędnych

Środkiem odcinka AB o współrzędnych A=(x_A,y_A) i B=(x_B, y_B) jest punkt:

(0)S= \frac{A+B}{2}= \left(\frac{x_A+x_B}{2}, \frac{y_A+y_B}{2}\right)

Twierdzenie 4

O odległości punktu od prostej

Odległość punktu P=(x_0,y_0) od prostej k danej równaniem ogólnym:

(0)Ax+By+C=0

wyraża się wzorem:

(0)d=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}

Twierdzenie 5

O środku ciężkości trójkąta

Współrzędne środka ciężkości S trójkąta ABC o współrzędnych A=\left(x_A,y_A\right), B=(x_B,y_B) i C=(x_C,y_C) wyrażają się wzorem:

(0)S=\left( \frac{x_A+x_B+x_C}{3}, \frac{y_A+y_B+y_C}{3} \right)

Definicja 1

Równanie kierunkowe prostej

Równanie postaci:

(0)y=ax+b

nazywamy równaniem kierunkowym prostej, gdzie a to współczynnik kierunkowy, a b - wyraz wolny.

Definicja 2

Kąt nachylenia prostej do osi OX

Kątem nachylenia prostej do osi OX nazywamy kąt którego wierzchołkiem jest punkt przecięcia się tej prostej z osią OX, a ramionami część prostej znajdująca się nad osia OX oraz półprosta zawierająca się w osi OX.

Twierdzenie 6

O kącie nachylenia prostej do osi OX

Prosta y=ax+b jest nachylona do osi OX pod kątem \alpha\in[0^\circ ,180^\circ )\setminus\{90^\circ \}, takim że \tg\alpha=a.

Twierdzenie 7

O związku współczynnika kierunkowego z kątem nachylenia prostej do osi OX

Kąt nachylenia prostej w postaci ogólnej y=ax+b do osi OX jest:

ostry, jeśli a>0,
zerowy (prosta jest równoległa do osi OX), jeśli a =0,
rozwarty, jeśli a<0.

Przykład 1

Przykład

Twierdzenie 8

O kącie między prostymi

Kąt ostry \alpha utworzony przez dwie nieprostopadłe proste o równaniach

(0)\begin{aligned} k: \ \ &y=ax_1+b_1\\ l:\ \ &y=ax_2+b_2 \end{aligned}

spełnia równanie:

(0)\tg\alpha=\left| \frac{a_1-a_2}{1+a_1\cdot a_2} \right|

Przykład 2

Przykład

Wiemy już, że współczynnik kierunkowy prostej zależy od kąta nachylenia tej prostej do osi OX:

(0)a=\tg \alpha

Żeby dwie proste były równoległe, nie mogą się przecinać, czyli ich kąt nachylenia do osi OX musi być taki sam, a tym samym współczynniki kierunkowe muszą być równe:

Twierdzenie 9

O równoległości prostych

Dwie proste o równaniach y=a_1x+b_1 oraz y=a_2x+b_2, gdzie a_1\neq0 i a_2\neq0 są równoległe wtedy i tylko wtedy, gdy a_1=a_2.

Twierdzenie 10

O prostopadłości prostych

Dwie proste o równaniach y=a_1x+b_1 oraz y=a_2x+b_2 są prostopadłe wtedy i tylko wtedy, gdy a_1\cdot a_2=-1.

Dowód

Niech dane będą dwie proste prostopadłe:

Mamy:

(0)\tg\beta=\tg\left(90^\circ +\alpha\right)=-\ctg\alpha=- \frac{1}{\tg\alpha}

Zatem

(0)\tg\beta=-\frac{1}{\tg\alpha}\Rightarrow\tg\beta \cdot \tg\alpha=-1\Rightarrow a_1 \cdot a_2=-1

Twierdzenie 11

Równanie prostej przechodzącej przez dwa punkty

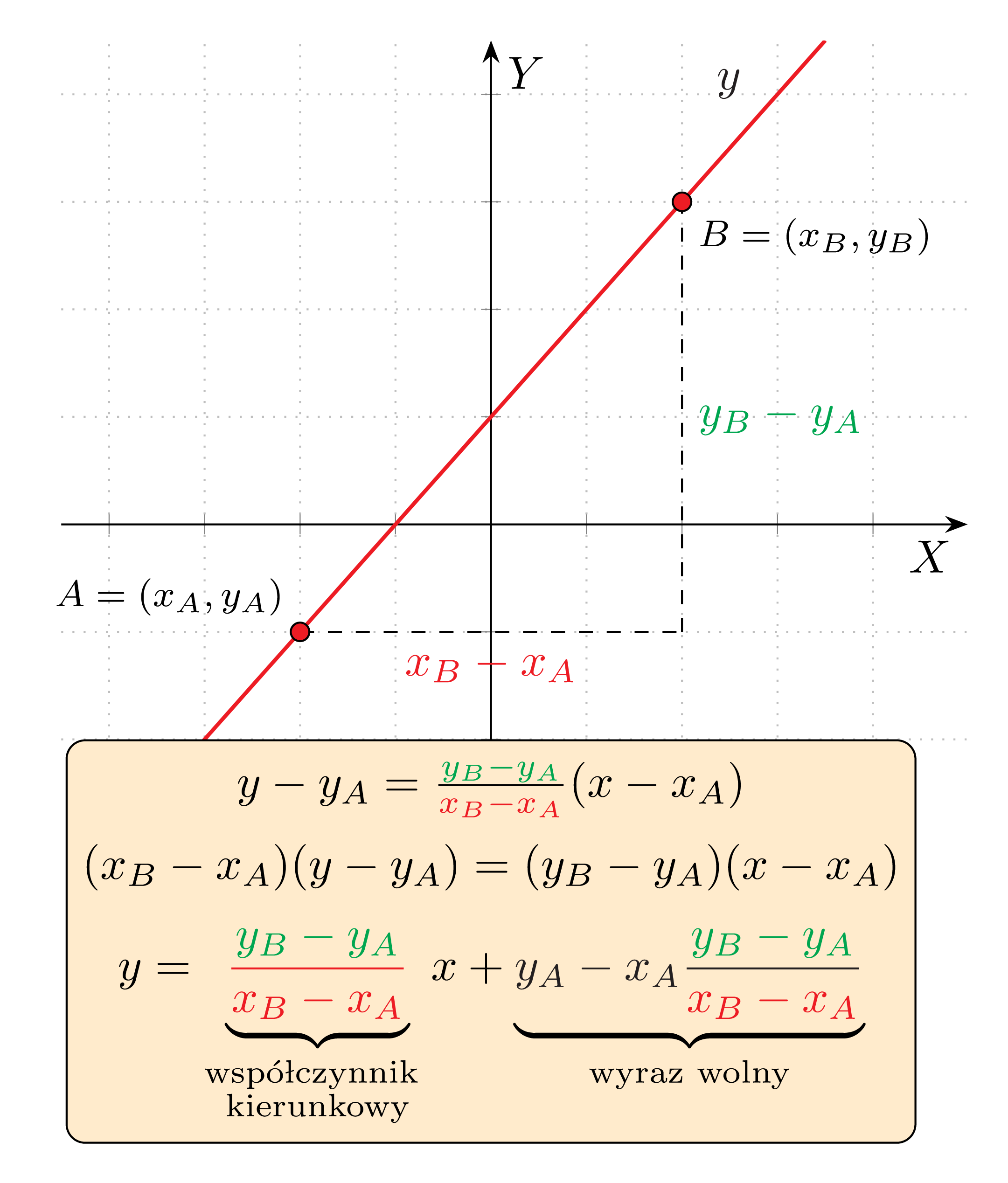
Równanie prostej przechodzącej przez punkty o współrzędnych (x_A,y_A) oraz (x_B,y_B) gdzie x_A\neq x_B, dane jest wzorem:

(0)y-y_A=\frac{y_B-y_A}{x_B-x_A}(x-x_A)

lub

(0)(x_B-x_A)(y-y_A)=(y_B-y_A)(x-x_A)

lub:

(0)y=\underbrace{\frac{y_B-y_A}{x_B-x_A}}_{\substack{\text{współczynnik }\\\text{kierunkowy}}}x+\underbrace{y_A-x_A\frac{y_B-y_A}{x_B-x_A}}_{\text{wyraz wolny}}

Uwaga 1

Uwaga

Jeśli powyższy wzór wydaje Ci się skomplikowany to nie bój się - w praktyce najczęściej wyznaczamy równanie prostej przechodzącej przed dwa punkty wprost z definicji prostej, podstawiając kolejno dwa podane punkty i otrzymując układ równań.

Warto jednak zapamiętać wzór

(0)(x_2-x_1)(y-y_1)=(y_2-y_1)(x-x_1)

i w razie potrzeby przekształcać go w celu wyznaczenia równania prostej.

Definicja 3

Równanie ogólne prostej

Równanie postaci

(0)Ax+By+C=0,

gdzie A^2+B^2\neq0 nazywamy równaniem ogólnym prostej.

Twierdzenie 12

O prostopadłości prostych w postaci ogólnej

Dwie proste o równaniach ogólnych A_1x+B_1+C_1=0 oraz A_2x+B_2+C_2=0 gdzie A_1^2+B_1^2\neq0 i A_2^2+B_2^2\neq0 są prostopadłe wtedy i tylko wtedy, gdy A_1A_2+ B_1B_2=0.

Twierdzenie 13

O równoległości prostych w postaci ogólnej

Dwie proste o równaniach ogólnych A_1x+B_1+C_1=0 oraz A_2x+B_2+C_2=0 gdzie A_1^2+B_1^2\neq0 i A_2^2+B_2^2\neq0 są równoległe wtedy i tylko wtedy, gdy A_1B_2+ A_2B_1=0.

Wzór na równanie prostej przechodzącej przez dwa punkty